Marcel Klinger & Daniel Thurm

Um konzeptuelles Wissen aufzubauen, können digitale Werkzeuge einen entscheidenden Beitrag leisten. Hierbei ist auch in den Blick zu nehmen, dass durch den Einsatz solcher Werkzeuge neue Aspekte verstärkt in den Fokus rücken, die in einem technologiefreien Unterricht weniger prominent sind. Hierzu zählt zum Beispiel der Aspekt der Achsenskalierung. Im Beitrag wird anhand linearer Funktionen exemplarisch aufgezeigt, wie das Thema „Achsenskalierung“ in einem technologiegestützen Unterricht adäquat berücksichtigt werden kann. Hierzu wird eine Lernumgebung vorgestellt, welche tragfähige Vorstellungen in diesem Bereich enwtickelt und so die Arbeit mit digitalen Werkzeugen integrativ unterstützt.

Einleitung

Digitale Werkzeuge im Mathematikunterricht bieten das Potential, einseitig kalkülorientierte sowie prozedurale Anteile im Unterricht zu reduzieren und einen verständnisorientierten und schülerzentrierten Unterricht zu fördern (z.B. Barzel, 2012; Zbiek et al., 2007). Insbesondere im Bereich der Funktionenlehre gibt es viele Einsatzmöglichkeiten, in denen z.B. durch einen häufigen Darstellungswechsel zwischen Term, Tabelle und Graph konzeptuelles Wissen der Schülerinnen und Schüler gefördert werden kann. Digitale Werkzeuge stellen dabei jedoch auch neue Anforderung an Lernende und Lehrende, die sich nicht nur auf der Ebene der technischen Fertigkeiten manifestieren. Insbesondere können Situationen entstehen, die es – mehr als in einem nicht rechnergestützten Unterricht – nötig machen, bestimmte Inhaltsbereiche auf einer tiefergehenden Ebene konzeptuell zu durchdringen. So stellen zum Beispiel viele digitale Werkzeuge Abszisse und Ordinate des Koordinatensystems in der Regel bereits in unterschiedlicher Skalierung dar, auch ohne dass dies durch eine Eingabe explizit an das Gerät kommuniziert wird. Dies führt bei Lernenden häufig zu Hürden, da hier nicht mehr notwendigerweise eine größere Steigung einer linearen Funktion mit einem steiler angezeigten Graphen einhergeht. Ausgehend von einer umfangreichen Studie mit mehr als 3000 Schülerinnen und Schülern wird im Folgenden anhand einer Lernumgebung gezeigt, wie solche kognitiven Konflikte gewinnbringend genutzt werden können, um fachliches Wissen zu fördern und tragfähige Vorstellungen zu entwickeln.

Ausgangslage

Der Einsatz digitaler Mathematikwerkzeuge im Mathematikunterricht wird sowohl von bildungsadministrativer Seite (vgl. KMK, 2015) als auch von Wissenschaft und Lehrkraftverbänden (vgl. DMV, GDM & MNU, 2008) empfohlen. Unter digitalen Werkzeugen versteht man dynamische Geometriesoftware, Tabellenkalkulationsprogramme, Funktionenplotter, Computer-Algebra-Systeme (CAS) sowie Multirepräsentationssysteme (Heinz et al., 2014) unabhängig von der äußeren Form, in der sie erscheinen. Denkbar sind Computer, Handhelds, z. B. Grafiktaschenrechner (GTR) oder Tablets (vgl. Barzel & Greefrath, 2015). Im Rahmen des Forschungsprojektes “GTR NRW” (Thurm, Klinger & Barzel, 2015 sowie www.gtr-nrw.de) haben im Bundesland Nordrhein-Westfalen etwa 3000 Schülerinnen und Schüler an zwei Leistungstests, welche den Inhaltsbereich “Funktionale Zusammenhänge” abdeckten, teilgenommen. Innerhalb der Testkonstruktion wurde besonderer Wert auf die Feststellbarkeit typischer Schülerfehler und des konzeptuellen Wissens in diesem Inhaltsbereich gelegt. Exemplarisch sei etwa auf das in Abb. 1 dargestellte Testitem verwiesen. Schülerinnen und Schüler werden hier mit der Situation konfrontiert, dass Abszisse und Ordinate des Koordinatensystems unterschiedliche Maßstäbe, d.h. eine unterschiedliche Skalierung, aufweisen. Von 2954 Schülerinnen und Schülern, die dieses Item bearbeitet haben, waren nur 51,6 Prozent in der Lage, eine passende Skalierung anzugeben. Es besteht somit der Verdacht, dass der Begriff des Koordinatensystems bei den entsprechenden Testteilnehmern nicht hinreichend konzeptualisiert wurde.

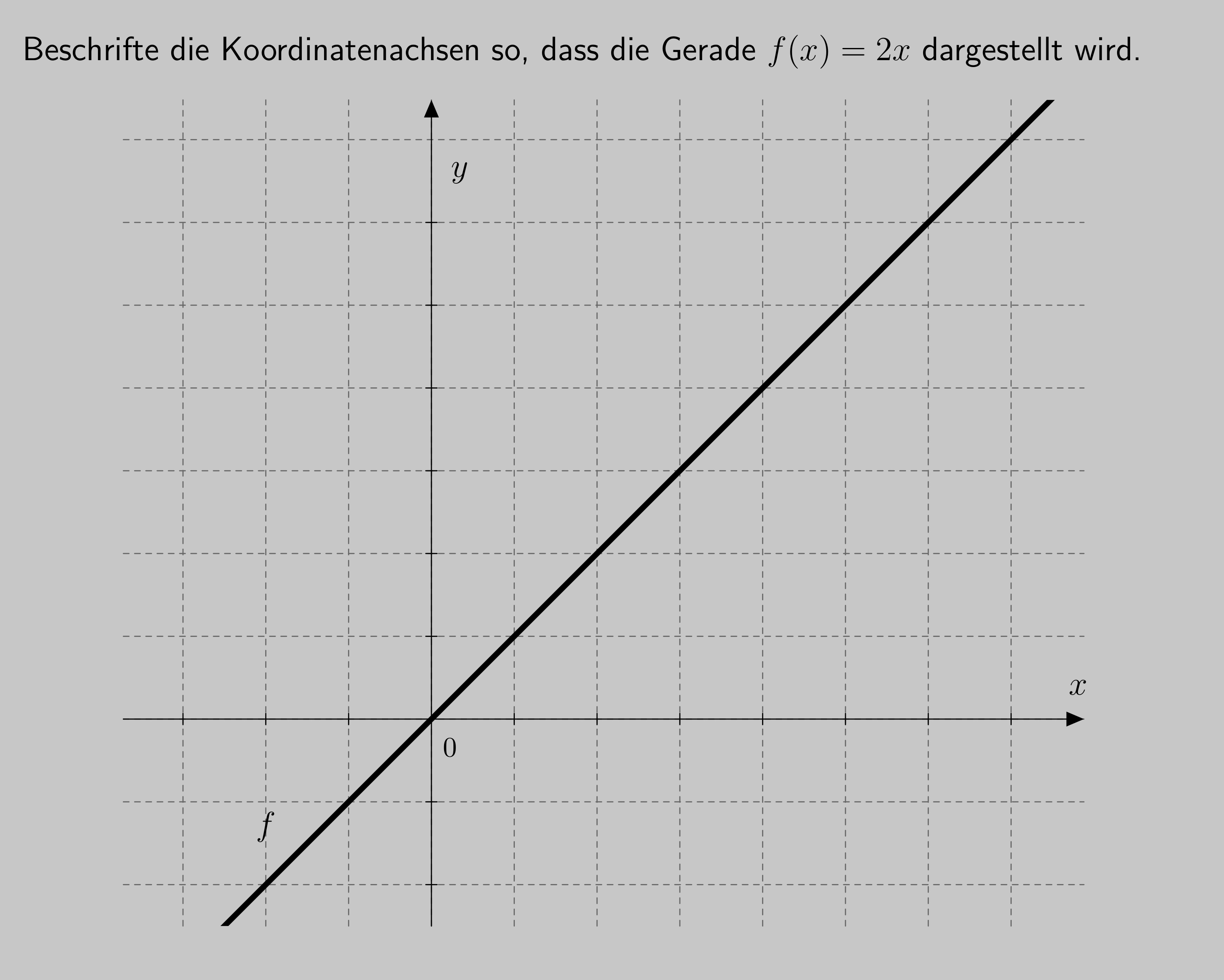
Abb. 1: Itembeispiel der im Rahmen von “GTR NRW” durchgeführten Schülertests

Dieses Ergebnis deckt sich auch mit anderen Forschungen. So haben Cavanagh und Mitchelmore sich bereits um die Jahrtausendwende dieser Thematik gewidmet und gezeigt, dass Schülerinnen und Schüler ein meist nur unzureichendes Verständnis von Koordinatensystemen haben. Insbesondere solche uneinheitlichen Skalierungen, die von der einheitlichen Standardskalierung abweichen, bereiteten ihnen größte Schwierigkeiten. In einer ähnlichen Situation wie der in Abb. 1 dargestellten zeigten nur zwei von 25 Schülerinnen und Schülern ein Verständnis von Koordinatensystemen, welches auch unterschiedliche Skalierungen zuließ: So war für 23 Lernende eine Darstellung wie in Abb. 1 untrennbar mit der Gleichung y=x verbunden (vgl. Cavanagh & Mitchelmore, 2000; Mitchelmore & Cavanagh, 2000).

Während ein derartiges Verständnis von Koordinatensystemen und unterschiedlichen Achsenskalierungen im klassischen und somit technologiefreien Unterricht meist nicht zum Problem wird, ist es beim Einsatz digitaler Werkzeuge essentiell zu berücksichtigen (vgl. Cavanagh & Mitchelmore, 2000). Wie bereits eingangs erwähnt, stellen Funktionenplotter Abszisse und Ordinate des Koordinatensystems je nach Funktionsgraph häufig in unterschiedlicher Skalierung dar, auch ohne dass dies durch eine Eingabe explizit an das Gerät kommuniziert wird (vgl. Vonder Embse & Engebretsen, 1996). Beispielsweise erscheint, je nach gewählter Achsenskalierung, die Normalparabel f(x) = x² wie eine stark gestauchte Parabel mit deutlich verringertem Vorfaktor (Abb. 2).

Nicht zuletzt ist der flexible Umgang mit uneinheitlich skalierten Koordinatensystemen (oder gar affin-transformierten oder nicht rechtwinkligen Koordinatensystemen) auch im täglichen Leben und in der damit verbundenen gesellschaftlichen Teilhabe von hoher Relevanz. So werden z.B. wirtschaftliche Datensätze häufig uneinheitlich skaliert dargestellt, insbesondere dann, wenn die in Beziehung gesetzten Daten in unterschiedlicher Größenordnung auftreten. Schülerinnen und Schülern ein tiefgreifendes Wissen über Koordinatensysteme zu vermitteln und sie zu befähigen, flexibel auch mit unterschiedlichsten Skalierungen umzugehen, ist daher unbedingt erstrebenswert.

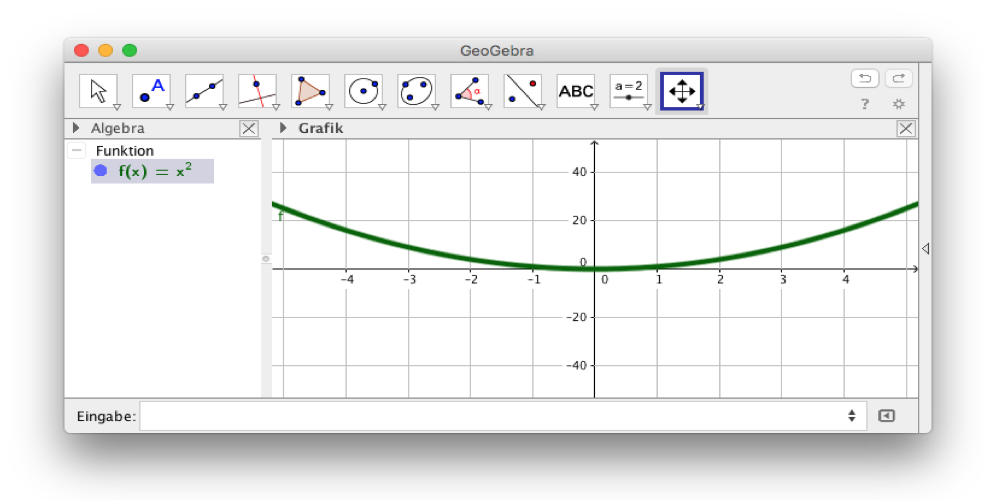
Abb. 2: Die Normalparabel erscheint mit entsprechender Achsenskalierung wie eine stark gestauchte Parabel.

Theoretischer Hintergrund

Um einen flexiblen Umgang mit unterschiedlichen Koordinatensystemen bei Schülerinnen und Schülern zu ermöglichen, ist ein stark ausgeprägtes konzeptuelles Wissen (z.B. Rittle-Johnson & Alibali, 1999; Prediger et al., 2011) bei den Lernenden vonnöten. Insbesondere hat ein adäquater Vorstellungsaufbau und die damit einhergehende Beseitigung etwaiger Fehlvorstellungen hohe Relevanz. Der Sachverhalt lässt sich hierbei gut mit dem von Tall und Vinner geprägten Begriff des “Concept Image” erklären. Für sie beschreibt es die vollständige kognitive Struktur, die mit einem Begriff verknüpft ist, insbesondere mentale Vorstellungen sowie hierzu gehörige Eigenschaften und Prozeduren. Ein solches Concept Image ist dabei nicht statisch zu verstehen. Vielmehr entwickelt es sich sukzessive über die Lebensspanne und ist ständigen Erweiterungen und Änderungen durch äußere Stimuli unterworfen (vgl. Tall & Vinner, 1981). Die entwickelten Vorstellungen müssen dabei nicht notwendigerweise korrekt sein. Sie können sogar in Konflikt zueinander stehen. Werden zwei solche Teile des Concept Image gleichzeitig ins Bewusstsein gerufen (Tall und Vinner sprechen vom Evoked Concept Image), entsteht ein mentaler Konflikt, der einen Lernenden ggfs. zum Nachdenken bewegt. So wird ein Kind über die Jahre eine entsprechende Vorstellung, ein Concept Image, eines Koordinatensystems aufbauen. Dieses hat sich anhand vieler Beispiele in der Schule etabliert.

Bei einer Schülerin oder einem Schüler könnte sich dabei das Bild manifestiert haben, dass Koordinatenachsen stets in den gleichen Größenverhältnissen skaliert sind. Cavanagh & Mitchelmore (2000) schlagen in diesem Zusammenhang die Unterscheidung zwischen einem „Relative“ und „Absolute Understanding“ von Skalierungen vor. Ersteres ist in seiner Konzeptualisierung fortgeschrittener zu verstehen und berücksichtigt nicht nur absolute Entfernungen zweier Markierungen auf den Koordinatenachsen, sondern setzt diese auch mit den entsprechenden aufgetragenen Wert ins Verhältnis. Letzteres ist hingegen von einer einseitigen Betrachtung geprägt; Schülerinnen und Schüler berücksichtigen in diesem Stadium lediglich die Entfernungen zweier Markierungen auf den Achsen oder die jeweiligen Werte, bringen jedoch nicht beides miteinander in Beziehung. Entsprechende verbale Äußerungen sind dann stark von Formulierungen geprägt, die lediglich auf Darstellungen in Standardskalierung zutreffen. Manipulationen der Skalierung werden – wenn überhaupt – nur in Form einer einheitlichen Vergrößerung oder Verkleinerung zugelassen, die der Multiplikation mit einem Faktor entsprechen (vgl. auch Mitchelmore & Cavanagh, 2000).

Werden unterschiedliche Skalierungen im Unterricht nicht thematisiert, bleibt das Concept Image von Schülerinnen und Schülern eher von einem absoluten Verständnis geprägt (vgl. Cavanagh & Mitchelmore, 2000). Erst wenn eine breitere Definition von Koordinatensystemen in den Unterricht eingeht, die auch solche subjektiven Widersprüche in Koordinatensystemen zulässt, kann sich das Concept Image des Lernenden erweitern, muss dies jedoch nicht (vgl. Vinner, 1983). Nur ein aktives Provozieren entsprechender Vorstellungsumbrüche zwingt Schülerinnen und Schüler, über andersartige Koordinatensysteme zu reflektieren und festigt gleichsam eine Erweiterung des Concept Images. Um dies entsprechend zu realisieren ist gutes Unterrichtsmaterial, z.B. in Form einer Lernumgebung, notwendig, welches die Lernenden aktiv-entdeckend und selbsttätig dazu aktiviert, ihre mentalen Modelle zu erweitern.

Lernumgebung

Ausgehend von den Ergebnissen der oben dargestellten Studie sowie des dargelegten theoretischen Hintergrundes wurde eine Lernumgebung konstruiert, welche besonders einen flexiblen Umgang mit und ein tiefgreifendes konzeptuelles Verständnis von Koordinatensystemen und der Darstellung von Funktionsgraphen in ihnen fokussiert.

Der Einstieg in die Lernumgebung erfolgt mit Hilfe zweier kontrastierender Darstellungen der Funktion f(x)=2x (s. Abb. 3). Umfasst das Concept Image der Schülerinnen und Schüler nicht den Aspekt, dass dieselbe lineare Funktion mit scheinbar verschieden steilen Geraden repräsentiert werden kann, werden die Lernenden an dieser Stelle zur Selbstreflexion angeregt. Durch einen so entstehenden kognitiven Konflikt wird ein bewusster Grundvorstellungsumbruch aktiv angeregt (vgl. dazu Vom Hofe & Wartha, 2004).

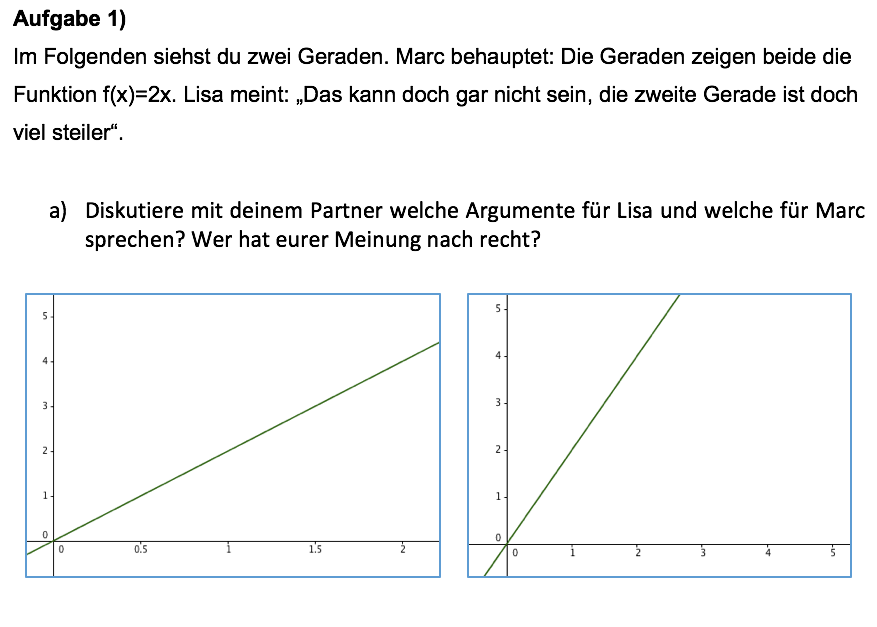
Abb. 3: Die erste Aufgabe der Lernumgebung zielt bei Schülerinnen und Schülern auf die Verursachung eines kognitiven Konflikts ab.

Eine tiefgreifendere Untersuchung der entsprechenden Thematik wird im Folgenden mit Hilfe digitaler Mathematikwerkzeuge ermöglicht. Die Lernenden erkunden die Auswirkungen unterschiedlicher Achsenskalierungen mit Hilfe eines interaktiven Arbeitsblattes (z.B. mit Hilfe von GeoGebra). Hierbei unterscheiden sie zwischen sich ändernden und invarianten Größen und verschriftlichen die beobachteten Phänomene (Abb. 4).

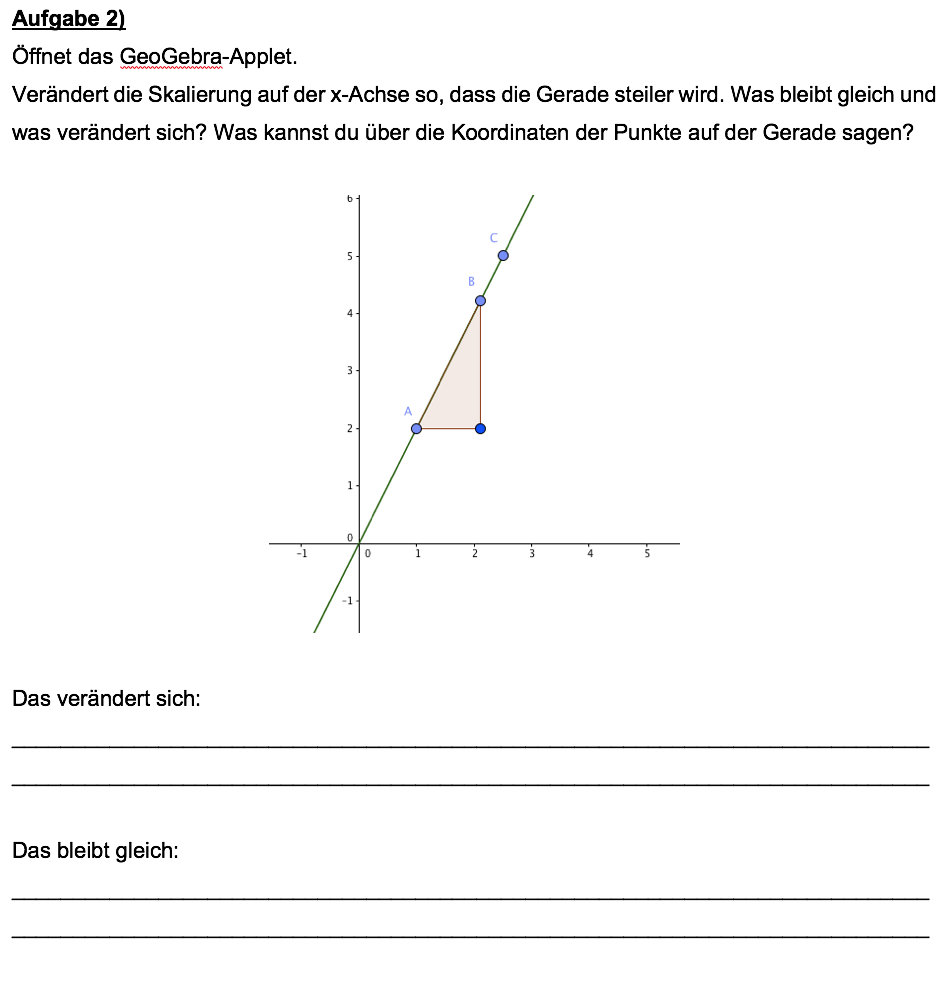
Abb. 4: Anhand eines GeoGebra-Applets erkennen die Schülerinnen und Schüler die Auswirkungen unterschiedlicher Achsenskalierungen auf die Gestalt des Graphen.

Im weiteren Verlauf der Lernumgebung festigen die Lernenden ihre bisherigen Erkenntnisse über unterschiedliche Skalierungen in einem „Funktionenmemory“. Hierbei befindet sich auf jeder Karte eine Darstellung eines Funktionsgraphen einer linearen Funktion. Solche Karten, die dieselbe mathematische Funktion darstellen, gelten als äquivalent. Damit das Spiel mit den üblichen Regeln funktioniert, sollte jede Funktion jeweils in einer geraden Anzahl vorhanden sein. Zur Binnendifferenzierung können leistungsstarke Schülerinnen und Schüler auch dazu angeregt werden, weitere eigene Memory-Karten zu erstellen.

Wichtig ist, dass zu gegebener Zeit gewonnene Erkenntnisse systematisiert und z.B. in Form eines Wissensspeichers gesichert werden (Prediger et al., 2011).

Mit einer weiteren Aufgabe wird die behandelte Thematik im Anschluss in einen Sachkontext eingebunden. Konkret sollen die Schülerinnen und Schüler den Stromtarif eines Energieanbieters graphisch darstellen. Hierbei sollen sie überlegen, welche Skalierungen für verschiedene Situationen sinnvoller sind. Ist der Energieverbrauch eines Konsumenten beispielsweise sehr gering, der betrachtete Zeitraum jedoch vergleichsweise lang, so ist es sinnvoll, die Zeitachse deutlich gröber zu beschriften als die Verbrauchsachse. Auch hier soll der Einsatz digitaler Werkzeuge das Arbeiten der Lernenden unterstützen. So können Graphen mit verschiedenen Skalierungen schnell generiert und hinsichtlich der Nützlichkeit reflektiert und diskutiert werden.

Diskussion und Ausblick

Die Theorie wie auch unsere Erfahrungen zeigen, dass früh angesetzt werden sollte, damit Schülerinnen und Schüler adäquate Vorstellungen von Koordinatensystemen ausprägen können. Im Sinne des Spiralprinzips sollte die Thematik dann regelmäßig aufgegriffen und auch im Kontext weiterer Funktionstypen thematisiert werden. Eine auf die unterschiedlichen Aspekte der Skalierung fokussierte Unterrichtsreihe, wie zum Beispiel die hier vorgestellte, sollte elementarer Bestandteil im Bereich der Funktionenlehre sein. Dabei erweisen sich insbesondere digitale Werkzeuge als wichtiges Hilfsmittel.

Insgesamt erweist sich die entwickelte Lernumgebung als ausgereift und gut funktionierend. Die Erfahrungen zeigen weiterhin, dass die Lernenden ihr Wissen über Koordinatensysteme erweitern und tragfähige Vorstellungen aufbauen können. So war z.B. ein flexiblerer Umgang mit Fenstereinstellung und Skalierungen bei der Arbeit mit digitalen Werkzeugen und bei der Bearbeitung von Modellierungsaufgaben zu beobachten. Wünschenswert wäre eine weitere empirische Untersuchung, um die Lernprozesse der Lernenden besser zu verstehen und darauf aufbauend die Lernumgebung weiter zu entwickeln.

Literatur

• Barzel, B. (2012). Computeralgebra im Mathematikunterricht: Ein Mehrwert – aber wann? Münster: Waxmann.
• Barzel, B. & Greefrath, G. (2015). Digitale Werkzeuge sinnvoll integrieren. In W. Blum (Hrsg.), Bildungsstandards Mathematik: konkret: Sekundarstufe II (S. 141–153). Berlin: Cornelsen Scriptor.
• Cavanagh, M. & Mitchelmore, M. (2000). Student misconceptions in interpreting basic graphic calculator displays. In T. Nakahara & M. Koyama (Hrsg.), Proceedings of the Conference of the International Group for the Psychology of Mathematics Education (Bd. 2, S. 161–168). Hiroshima: PME.
• DMV, GDM & MNU (2008). Standards für die Lehrerbildung im Fach Mathematik: Empfehlungen von DMV, GDM und MNU, Juni 2008. Mitteilungen der DMV 16, 149–159.
• Heintz, G., Elschenbroich, H.-J., Laakmann, H., Langlotz, H., Schacht, F. & Schmidt, R. (2014). Digitale Werkzeugkompetenzen im Mathematikunterricht. Der mathematische und naturwissenschaftliche Unterricht 67(5), 300–306.
• KMK (Sekretariat der Ständigen Konferenz der Kultusminister der Länder der Bundesrepublik Deutschland) (2015). Bildungsstandards im Fach Mathematik für die Allgemeine Hochschulreife (Beschluss der Kultusministerkonferenz vom 18.10.2012). Köln: Kluwer.
• Mitchelmore, M. & Cavanagh, M. (2000). Students‘ difficulties in operating a graphics calculator. Mathematics Education Research Journal 12(3), 254–268.
• Prediger, S., Barzel, B., Leuders, T. & Hußmann, S. (2011). Systematisieren und Sichern: Nachhaltiges Lernen durch aktives Ordnen. Mathematik Lehren 164, 2–9.
• Rittle-Johnson, B. & Alibali, M. W. (1999). Conceptual and procedural knowledge of mathematics: Does one lead to the other? Journal of Educational Psychology 91(1), 175–189.
• Tall, D. & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics 12(2), 151–169.
• Thurm, D., Klinger, M. & Barzel, B. (2015). How to professionalize teachers to use technology in a meaningful way – design research of a CPD program. In N. Amado & S. Carreira (Hrsg.), Proceedings of the 12th International Conference on Technology in Mathematics Teaching (S. 335–343). Faro: University of Algarve.
• Vinner, S. (1983). Concept definition, concept image and the notion of function. International Journal of Mathematical Education in Science and Technology 14(3), 293–305.
• Vom Hofe, R. & Wartha, S. (2004). Grundvorstellungsumbrüche als Erklärungsmodell für die Fehleranfälligkeit in der Zahlbegriffsentwicklung. In Beiträge zum Mathematikunterricht 2004: Vorträge auf der 38. Tagung für Didaktik der Mathematik vom 1. bis 5. März 2004 in Augsburg (S. 593–596). Hildesheim: Franzbecker.
• Vonder Embse, C. & Engebretsen, A. (1996). Friendly windows for graphing calculators. Mathematics Teacher 86(6), 508–511.
• Zbiek, R. M., Heid, M. K., Blume, G. W. & Dick, T. P. (2007). Research on technology in mathematics education – A perspective of constructs. In F. K. Lester (Hrsg.), Second handbook of research on mathematics teaching and learning (S. 1169–1207). Charlotte: Information Age.

(erschienen in: Klinger, M. & Thurm, D. (2016). Zwei Graphen aber eine Funktion? – Konzeptuelles Verständnis von Koordinatensystemen mit digitalen Werkzeugen entwickeln. transfer Forschung ↔ Schule, 2(2), 225–232. – DOI: 10.17185/duepublico/44812)