Im Rahmen der Dissertation von Klinger (2018) wurde das FALKE-Testinstrument entwickelt (Funktionales Denken und Analysis – Lernen von Konzepten in der Einführungsphase, s. z.B. www.falke-test.de), welches das Schülerverständnis von Konzepten im ersten Jahr der Oberstufe (in Nordrhein-Westfalen die sog. Einführungsphase) fokussiert. Der Test befindet sich inhaltlich somit an der Nahtstelle zwischen der Funktionenlehre der Sekundarstufe I und der frühen Analysis samt des Differentialrechnungskonzepts der Oberstufe. Der vorliegende Beitrag skizziert das theoretische Konstrukt, welches der Entwicklung des verstehensorientierten Testinstruments zugrunde lag.
Testtheoretischer Fokus
Der Begriff Verständnis wird im Rahmen des FALKE-Tests vor allem durch einen Fokus auf spezifische fachdidaktische Konzepte operationalisiert. So sollten Lernende einerseits unterschiedliche Grundvorstellungen funktionaler Zusammenhänge ausbilden, welche im Allgemeinen in die Kategorien Zuordnungsvorstellung (Z), Kovariationsvorstellung (K) sowie Objektvorstellung (O) gegliedert werden. Andererseits sind auch entsprechende Grundvorstellungen der Ableitungsfunktion von Bedeutung, namentlich die Änderungsratenvorstellung (A), Tangentensteigungsvorstellung (T) sowie Lokale-Linearisierungsvorstellung (L) (Hußmann & Prediger 2010). Ferner wird innerhalb einschlägiger Literatur die Relevanz unterschiedlicher Darstellungsformen funktionaler Zusammenhänge hervorgehoben: Hierbei fasst insbesondere Duval (2006) jede Form mathematischer Tätigkeit als den Wechsel zwischen entsprechenden Repräsentationen auf. Es werden gemein hin die situativ-sprachliche (S), graphisch-visuelle (G), formal-symbolische (A) sowie numerisch-tabellarische Darstellungsform unterschieden. Weiterhin müssen Lernende versiert im Umgang mit funktionalen Zusammenhängen auf den unterschiedlichen Ebenen, die für die Einführungsphase relevant sind, sein. Hiermit ist gemeint, dass flexibel zwischen der üblichen Funktionsebene (F) sowie der Ebene der differenzierten Funktion (D) aber auch der Ebene einer manipulierten Funktion (M) gewechselt werden kann (vgl. tlw. Hahn 2008). Letztere umfasst dabei eine operative Veränderung einer Ausgangsfunktion, die nicht durch Differentiation, sondern durch das Wirken einer Transformation oder direkte Manipulation der entsprechenden Funktionsparameter der Term-Darstellung geschieht (vgl. Klinger 2018, S. 119 ff.).
Konzeption
Obige Ausführungen bilden die Grundlage einer zielgerichteten Aufgabenkonstruktion. Zur Wahrung der Repräsentativität des entwickelten Itemsets wurden alle Items in ein entsprechendes Klassifikationsmodell verortet, welches in Abbildung 1 dargestellt ist und sich aus den zuvor genannten Theorieaspekten ergibt. Hierbei wurde auf die numerisch-tabellarische Form insgesamt sowie auf die Implementation der Richtung der Darstellungswechsel u.a. zu Gunsten einer Komplexitätsreduktion hinsichtlich der Testentwicklung verzichtet (vgl. Klinger 2018, S. 184 ff.). Weiterhin lässt sich die Ebene „differenzierte Funktion“ ihrerseits entlang der drei oben genannten Grundvorstellungen zum Ableitungsbegriff zerlegen.
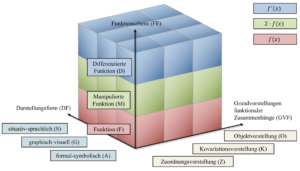
Abb. 1: Theoretisches Klassifikationsmodell für eine zielgerichtete Entwicklung und Kategorisierung verstehensorientierter Leistungstestaufgaben
Das Testinstrument ist so konzipiert, dass ein erster Teiltest zu Beginn, ein zweiter gegen Ende der Einführungsphase eingesetzt werden kann. Entsprechend wurden Items anhand des Rasters entwickelt, die den spezifischen curricularen Anforderungen genügen. Während die Items des ersten Tests daher nur die Funktionsebene F fokussieren, umfasst der zweite Test auch Items, die sich auf den Funktionsebenen D und M verorten lassen.
Vorstellungen beim Differenzieren
Aufgaben erfordern zu ihrer Bearbeitung die jeweiligen Vorstellungen (im deskriptiven Sinne des Grundvorstellungsbegriffs), den Umgang mit entsprechenden Darstellungen sowie einen Wechsel der Funktionsebenen in vielfältiger und individuell von der Aufgabe abhängiger Weise. Exemplarisch seien hierzu Aufgaben zum Differenzieren herangezogen: Solchen Aufgaben ist gemein, dass sie stets einen Wechsel der betrachteten Funktionsebene erfordern (konkret zwischen den Ebenen F und D). In Abhängigkeit von den jeweiligen Erfordernissen entsprechender Aufgaben und der damit verbundenen Art und Weise wie differenziert wird, stehen hierbei unterschiedliche Grundvorstellungen funktionaler Zusammenhänge auf den jeweiligen Funktionsebenen im Mittelpunkt. Dabei fassen wir sowohl Zuordnungs- als auch Kovariationsvorstellung als innerhalb der Objektvorstellung gekapselt auf. Je nach Charakteristik des Ableitungsprozesses können die erstgenannten Vorstellungen dann bei Bedarf aus dem die Funktion umfassenden Objekt entkapselt werden (Dubinsky & Harel 1992). Abbildung 2 hebt jene der drei Grundvorstellungen zu Funktionen, die sich ihrerseits auf beiden beteiligten Funktionsebenen realisieren, für drei unterschiedliche Arten des Differenzierens hervor.
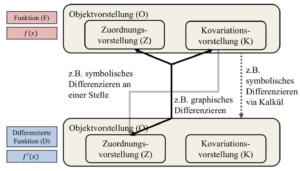
Abb. 2.: Funktionsebenen- und Aspektwechsel in der Analysis in erweiterter Betrachtung (abgewandelt entnommen aus Klinger 2018, S. 129)
Konkret stehen etwa beim symbolischen Differenzieren an einer Stelle, wie es häufig während der unterrichtlichen Heranführung an den Ableitungsbegriff Gegenstand von Schulbuchaufgaben ist, die Kovariationsvorstellung auf Ebene F und die Zuordnungsvorstellung auf Ebene D im Vordergrund. Zuvor muss die gegebene Funktion zunächst ggfs. mental entkapselt werden, d.h. von der Objekt- auf die zuvor genannten Vorstellungen geschlossen werden. Im Kontrast hierzu ist beim symbolischen Differenzieren mittels Ableitungskalkül keine Entkapselung notwendig, so dass ausschließlich die Auffassung als Objekt hervorgehoben wird, sofern Lernende überhaupt Vorstellungen mit dieser Tätigkeit verbinden (vgl. Klinger 2018, S. 103 ff.). Im Rahmen des graphischen Differenzierens muss formelfrei von einem Funktionsgraphen auf den entsprechenden Graphen der Ableitungsfunktion geschlossen werden. Da einerseits charakteristische Punkte der Funktionen wie auch das spezifische Wachstumsverhalten beider Funktionen in Einklang gebracht werden müssen, handelt es sich um eine besonders vorstellungsintensive Tätigkeit innerhalb der Analysis (Hußmann & Prediger 2010).
Exemplarisch zeigt Abbildung 3 ein Item zum graphischen Differenzieren des zweiten Tests sowie die durch diese Aufgabe akzentuierten Teilelemente des beschriebenen Modells. Wie bereits oben ausgeführt, stehen Zuordnungs- und Kovariationsvorstellung unter besonderem Fokus sowie die Funktionsebenen F und D. Seiner Natur nach ist die graphisch-visuelle Darstellungsform von besonderer Bedeutung.
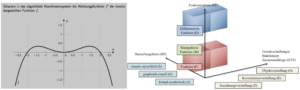
Abb. 3: Beispielitem zum graphischen Differenzieren (links) und Verortung innerhalb des dreidimensionalen Modells aus Abbildung 2 (rechts)
Analog lassen sich auch alle weiteren Items bzgl. ihrer jeweiligen Erfordernisse aus fachdidaktischer Perspektive innerhalb des vorgestellten Modells verorten.
Fazit
Im Schuljahr 2014/15 wurden die FALKE-Tests großflächig im Raum Nordrhein-Westfalen eingesetzt. Hierbei konnten für den ersten insgesamt 3202 (50.0% w., 49.5% m.), für den zweiten Test insgesamt 2665 (48.9% w., 50.3% m.) Schülerinnen und Schüler erfasst werden. Während der Testentwicklung aber auch im Nachgang im Rahmen der Analyse der gewonnenen Daten erwies sich das vorgestellte theoretische Konstrukt zur zielgerichteten Testentwicklung als geeignetes Werkzeug.
Literatur
- Dubinsky, E. & Harel, G. (1992). The nature of the process conception of function. In G. Harel & E. Dubinsky (Hrsg.), The concept of function: Aspects of epistemology and pedagogy (S. 85–106). Washington: Mathematical Association of America.
- Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61(1–2), 103–131.
- Hahn, S. (2008). Bestand und Änderung: Grundlegung einer vorstellungsorientierten Differentialrechnung. Oldenburg: Didaktisches Zentrum.
- Hußmann, S. & Prediger, S. (2010). Vorstellungsorientierte Analysis – auch in Klassenarbeiten und zentralen Prüfungen. Praxis der Mathematik in der Schule, 52(31), 35–38.
- Janvier, C. (1978). The interpretation of complex cartesian graphs representing situations: Studies and teaching experiments (Dissertation, University of Nottingham, Nottingham).
- Klinger, M. (2018). Funktionales Denken beim Übergang von der Funktionenlehre zur Analysis: Entwicklung eines Testinstruments und empirische Befunde aus der gymnasialen Oberstufe. Wiesbaden: Springer Spektrum.
(erschien in: Klinger, M. & Barzel, B. (2018). Zielgerichtete Entwicklung von verstehensorientierten Leistungstestaufgaben am Beispiel des Funktionalen Denkens in der frühen Analysis der Oberstufe. In Fachgruppe Didaktik der Mathematik der Universität Paderborn (Hrsg.), Beiträge zum Mathematikunterricht 2018(Bd. 2, 983–986). Münster: WTM-Verlag. – DOI: 10.17877/DE290R-19457)