Marcel Klinger & Bärbel Barzel

Am Ende der Schulzeit bleiben bei vielen Schülerinnen und Schülern oft nur leere Begriffshülsen mathematischer Konzepte. Um hier Abhilfe zu schaffen, müssen Lernende den inhaltlichen Kern der Begriffe wirklich verstehen. Wie dies gelingen kann und welche Hürden Schülerinnen und Schüler dabei nehmen müssen, erläutert der Artikel am Beispiel des Funktionsbegriffs.

Was würden Sie auf die folgende Frage antworten?

„Max ist Maler. In letzter Zeit sollte er oft weihnachtliche Bilder an Schaufenster malen. Erst gestern malte er einen 56 cm großen Weihnachtsmann an das Fenster einer Bäckerei. Dafür benötigte er 6 ml Farbe. Nun soll er eine vergrößerte Version desselben Bildes an eine Supermarktscheibe malen. Diese Kopie soll 168 cm hoch werden. Wie viel Farbe benötigt Max vermutlich?“ (De Bock et al. 2007, S. 92, Übersetzung nach Klinger 2018, S. 252).

Abb. 1: Darstellung zweier Weihnachtsmänner (entnommen aus De Bock et al. 2007, S. 92)

Die meisten Kinder einer kleinen Gruppe von Schülerinnen und Schülern, die die belgischen Forscher um De Bock et al. (2007) befragten und ihnen zusätzlich die in Abbildung 1 dargestellte Grafik vorlegten, antworteten „18 ml“. Diese Lösung erhält man, wenn man davon ausgeht, dass die Menge der benötigten Farbe sich linear zur Höhe des gewünschten Weihnachtsmannbildes verhält. In diesem Fall unterliegt man einer Illusion von Linearität.

Auf die richtige Antwort kam hingegen kaum ein Lernender: Findet die Vergrößerung der Grafik wie dargestellt in nicht verzerrender Weise statt, muss sowohl die Höhe als auch die Breite des Bildes entsprechend des Faktors 3 vergrößert werden. Entsprechend muss man davon ausgehen, dass sich auch der Farbverbrauch jeweils verdreifacht, so dass insgesamt mit einer Verneunfachung zu rechnen ist. Korrekt wäre also die Angabe „54 ml“.

Ähnliche Probleme mit dieser Aufgabe hatten auch über 3000 Schülerinnen und Schüler, die im Rahmen des FALKE-Tests, den wir unten noch genauer beschreiben, in der Einführungsphase der Oberstufe befragt wurden.

Was steckt dahinter? Das Denken in Zusammenhängen zwischen einer unabhängigen und einer davon abhängigen Größe birgt für viele Lernende Probleme. Dabei sind wir im Alltag von vielen solcher Zusammenhänge umgeben: Der Benzinverbrauch eines Autos hängt von der gefahrenen Geschwindigkeit ab; die Stromkosten steigen durch viele angeschaltete Verbrauchsgeräte; die Höhe des Schaums eines frisch gezapften Bieres reduziert sich mit der Zeit, usw.  In der Mathematik spricht man von funktionalen Zusammenhängen, wenn klar ist, welche Werte die unabhängige Variable annehmen kann und wenn zu jedem Wert der unabhängigen Größe genau ein Wert der abhängigen Größe gehört, so wie es etwa zu jeder Anzahl gefahrener Kilometer genau einen Wert für den Benzinverbrauch gibt.

Ein gewisses Bewusstsein für derartige funktionale Beziehungen ist eine erstrebenswerte Kompetenz, die nicht nur innerhalb der Mathematik von besonderer Relevanz ist. Tatsächlich durchziehen solche Zusammenhänge auch das alltägliche Leben. Häufig werden sie in Grafiken und Diagrammen dargestellt und sind bedeutsam für berufliche Bildung und die Fähigkeit zur gesellschaftlichen Teilhabe. Aus diesem Grund ist die Untersuchung funktionaler Abhängigkeiten bereits seit über einhundert Jahren Bestandteil deutscher Mathematik-Curricula. So forderte der bekannte deutsche Mathematiker Felix Klein bereits im Rahmen der Reformvorschläge von Meran im Jahr 1905 die „Erziehung zur Gewohnheit des funktionalen Denkens“ (Krüger 2000, S. 5) und damit verbunden die curriculare Integration des Funktionsbegriffs als eine der unterrichtlichen Kernideen der Mathematik.

Heute findet sich diese Forderung in der sog. Leitidee „Funktionaler Zusammenhang“ in den Bildungsstandards der Kultusministerkonferenz (KMK) wieder. Hier heißt es für die Sekundarstufe I u.a.: „Die Schülerinnen und Schüler nutzen Funktionen als Mittel zur Beschreibung quantitativer Zusammenhänge.“ (KMK 2004)

Doch was genau sollte zu funktionalen Zusammenhängen gelernt werden, damit nicht nur die Illusion von Linearität sondern auch andere Hürden vermieden und ein flexibler Umgang mit funktionalen Zusammenhängen gelernt wird?

Vorstellungen aufbauen: Begriffe mit Leben füllen

Der Begriff „Funktion“ ruft bei vielen Menschen, deren postschulische Lebenswelt eine eher geringe Schnittmenge mit der Funktionenlehre aufweist, häufig nur bruchstückhafte Erinnerungen hervor. Befragt man Erstsemester, nennen viele nur die Symbolik f(x) oder bestimmte Funktionstypen (wie lineare oder quadratische Funktionen). Oft ist noch bekannt, dass man für  verschiedene Zahlen einsetzen oder zur Funktion einen Funktionsgraphen anfertigen kann. Andere Dinge sind möglicherweise in Vergessenheit geraten, etwa wie man die Nullstellen einer Funktion dritten Grades berechnet oder den Schnittpunkt einer Parabel und einer Geraden bestimmt.

Aber nicht nur die konkrete Berechnung von Nullstellen oder Schnittpunkten stellt für viele Menschen eine Herausforderung dar. Vor allem verbinden sie häufig keine Vorstellung mit dem zugrundeliegenden funktionalen Zusammenhang, womit sich ein tiefergehender Einblick in dahinterliegende Konzepte der Mathematik meist verwehrt. Fehlende Vorstellungen können umgekehrt der Auslöser dafür sein, dass erlernte Prozeduren und reines Faktenwissen schnell in Vergessenheit geraten, da mit ihnen kein Sinn verbunden wird.

Aufgabe der Fachdidaktik Mathematik ist es u.a., Ansätze zu entwickeln, die der Vermittlung umfänglichen und vor allem möglichst langfristigen mathematischen Kompetenzen dienen. Dies kann nicht ausschließlich durch die Vermittlung einer Definition, sondern nur, wenn die Ausbildung sinnstiftender Vorstellungen zu einem mathematischen Begriff in den Blick genommen wird, gelingen (vgl. z.B. Vollrath 2014; Barzel et al. 2013). Zentral ist hierbei die Idee, den Mathematikunterricht keinesfalls als plumpes Auswendiglernen von Zusammenhängen oder als Anleitung zur Durchführung mathematischer Verfahren und Algorithmen zu verstehen, sondern Verständnis für die Zusammenhänge, Strukturen, Definitionen und Konventionen der Mathematik zu konstituieren. Mit dem Begriff des Verständnisses ist nicht nur gemeint, die entsprechenden mathematischen Inhalte möglichst tiefgreifend zu durchdringen. Der Begriff kann auch in jenem Sinne aufgefasst werden, wie man jemandem Verständnis für etwas entgegenbringt: So sollten Schülerinnen und Schüler im Idealfall auch Verständnis dafür aufzubringen lernen, warum Mathematikerinnen und Mathematiker jene Begriffe ihres Unterrichts so geformt haben, wie sie heute sind.

Arbeiten, die sich mit dem Ziel des Vorstellungsaufbaus beschäftigen, haben innerhalb der deutschsprachigen Mathematikdidaktik eine lange Tradition. Als Resultat einer begrifflichen Ausschärfung in der Geschichte der Mathematikdidaktik hat sich heute das Konzept der Grundvorstellungen weitgehend etabliert (vgl. vom Hofe 1995): Man geht davon aus, dass für einen mathematischen Begriff einige wenige Vorstellungen von besonderer Bedeutung sind – eben solche Grundvorstellungen. Hierbei handelt es sich i.d.R. um zwei bis fünf Grundvorstellungen zu einem Konzept oder einer Operation, die inzwischen für viele mathematische Begriffe der Schule ausgearbeitet und im Rahmen mathematikdidaktischer Forschung konsolidiert sind. In diesem Sinne sind Grundvorstellungen aus normativer und somit vom mathematischen Stoff her eingenommene Perspektive zu verstehen, d.h. als eine möglichst vollständige und im Wesentlichen von der Theorie ausgehenden Zusammenstellung solcher Vorstellungen, die für die Idee eines mathematischen Begriffs am wesentlichsten sind. Hierbei handelt es sich gewissermaßen um einen Soll-Zustand. Nimmt man hingegen die Perspektive der Lernenden ein, fragt man also danach, welche Grundvorstellungen ein Lernender ausgebildet oder erworben hat, spricht man von einer deskriptiven Perspektive. Diese entspricht somit dem Ist-Zustand.

Für das Funktionskonzept sind verschiedene solcher Vorstellungen von ganz besonderer Bedeutung. Speziell für den Funktionsbegriff finden sich innerhalb der mathematikdidaktischen Literatur gemein hin drei Grundvorstellungen funktionaler Zusammenhänge: Funktion als Zuordnung, Funktion als Kovariation, Funktion als ein Ganzes (Vollrath 2014).

Für jede einzelne dieser Grundvorstellungen sind besondere Aspekte des Funktionskonzepts ausschlaggebend, etwa dass – wie oben schon genannt – zu jedem x-Wert ein y-Wert bestimmt werden kann. Man betrachtet die Funktion als Zuordnung (vgl. Malle 2000; Vollrath 2014). Diese Vorstellung findet sich auch in der mathematischen Definition wieder:  Eine Funktion ordnet jedem Wert ihrer Definitionsmenge genau ein Element ihrer Wertemenge zu. Im Beispiel des gezapften Bieres gehört so zu jedem Zeitpunkt, an dem gemessen wird, eine bestimmte Höhe des Bierschaums.

Andererseits geht es nicht bloß um eine solche lokale Perspektive in Form reiner Zuordnungen und somit isolierte Wertepaare. Stattdessen findet ein Wechselspiel zweier Größen statt, die miteinander kovariieren. Bei dieser eher global-dynamischen Sicht auf funktionale Zusammenhänge geht es um ebendiese Kovariation, d.h. die Art der Interaktion zwischen beiden Größen (vgl. Malle 2000; Vollrath 2014). So wird beispielsweise beim Bierschaum gelten: Je mehr Zeit vergeht, desto weniger Schaum bleibt übrig. Es findet also ein Zerfall statt. Interessant ist, wie dieser Prozess genau aussieht. Wie schnell vollzieht sich der Zerfall? Ist er immer gleich schnell oder mal langsamer? Konkrete Messungen können hier erste Anhaltspunkte geben. Durch reale Messungen, wie sie in Abbildung 2 dargestellt sind, wird nicht nur die Zuordnung sondern gerade auch die Kovariation von Schülerinnen und Schülern besser erfasst (Ganter 2013).

Eine Möglichkeit, den Verlauf anschaulich zu erfassen, bietet der entsprechende Funktionsgraph des betrachteten funktionalen Zusammenhangs, der näherungsweise ebenfalls in Abbildung 2 gezeigt ist. Mit seiner Hilfe kann man den Prozess in seiner Gänze betrachten und viele Teilinformationen ablesen. Eng verbunden hiermit ist die dritte ausgezeichnete Vorstellung funktionaler Zusammenhänge, bei der es darum geht, diesen als Ganzes oder als Objekt zu betrachten. Diese Vorstellung tritt immer dann in den Vordergrund, wenn Menschen eine Funktion in ebendieser Gänze betrachten und ihr Legitimität als eigenständiges Objekt gewähren (vgl. Vollrath 2014). Das ist beispielsweise der Fall, wenn man zu bestimmten Funktionsarten einen typischen Graphen vor Augen hat, wie beispielsweise eine Gerade zu einer linearen Funktion, eine Parabel zu einer quadratischen Funktion. Beim Betrachten der Messwerte zum Bierschaum könnte man hier etwa an den Graphen einer Exponentialfunktion denken. Das würde bedeuten, dass der Zerfall sich exponentiell vollzieht, d.h. pro Zeiteinheit sich der Schaum um einen konstanten Faktor reduziert. Zumindest liefert eine Exponentialfunktion ein annähernd passendes Modell. Hier ist jedoch Vorsicht geboten: Im konkreten Beispiel des Bierschaumzerfalls konnte Theyßen (2009) plausibel darlegen, dass physikalische Gründe gegen einen exponentiellen Zerfall sprechen, auch wenn das mathematische Modell der Exponentialfunktion für die gemessene Zeit gut zu passen scheint.

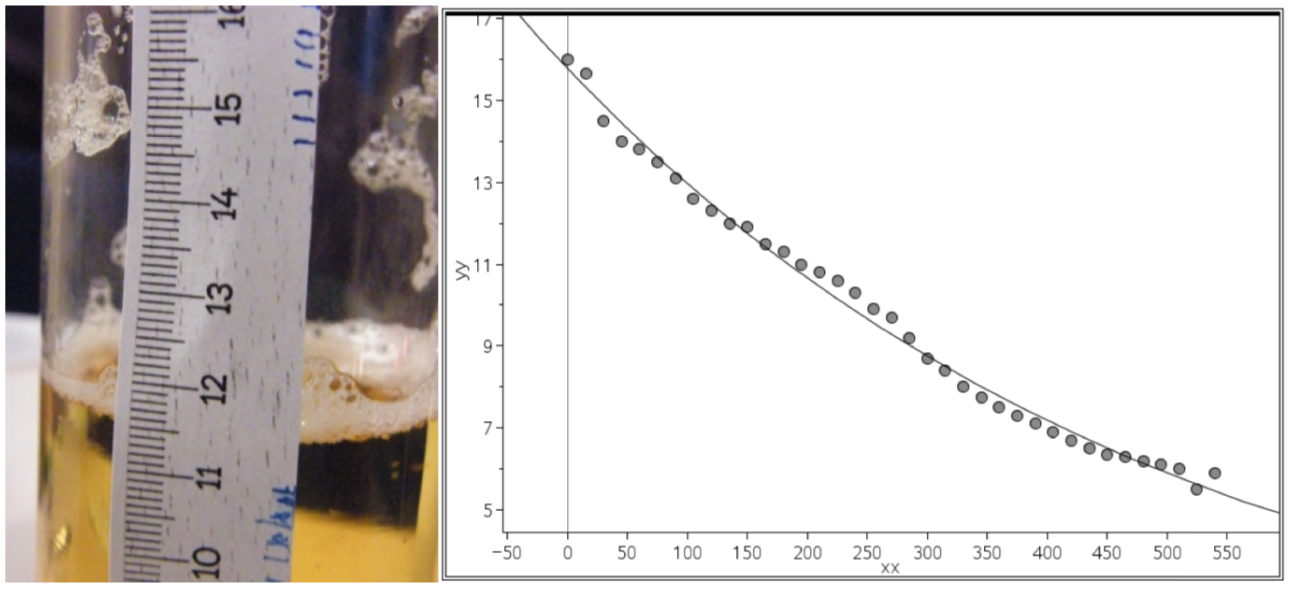
Abb. 2: Messen der Höhe des Bierschaums in Abhängigkeit von der Zeit. Der dargestellte Funktionsgraph bietet eine gute Übersicht über die generelle Natur des ihm inhärenten funktionalen Zusammenhangs.

Bei den drei genannten Vorstellungskategorien handelt es sich entsprechend des Grundvorstellungskonzepts um den inhaltlichen Kern und somit das wesentliche Bild, das Schülerinnen und Schüler von Funktionen im Laufe ihrer Unterrichtszeit idealerweise erwerben. Die Relevanz der drei Kategorien spiegelt sich auch in einem sie umfassenden Oberbegriff wider: So bilden die genannten Grundvorstellungen funktionaler Zusammenhänge die wichtigsten Charakteristika des sog. Funktionalen Denkens (vgl. z.B. Vollrath 1989).

Repräsentationen: Für die Mathematik mehr als ein Hilfsmittel zur Veranschaulichung

Neben den bereits beschriebenen Grundvorstellungen funktionaler Zusammenhänge hat noch ein anderes Konzept eine wichtige Bewandtnis für den Funktionenbegriff im Speziellen und für die Mathematik insgesamt: Anders als in den Naturwissenschaften sind mathematische Konstrukte wie jenes der Funktion abstrakt und physisch nicht existent. Messungen wie beim Bierschaumzerfall sind nur Wege, die mathematischen Konzepte wie zum Beispiel Eindeutigkeit der Zuordnung, Änderungsrate, unabhängige und abhängige Größe begreifbar zu machen. Diesem Zusammenhang ist es geschuldet, dass Repräsentationen bzw. Darstellungen, also etwas, das für etwas anderes steht, in der Mathematik und insbesondere auch der Mathematikdidaktik von besonderer Bedeutung sind.

Konkret sind für den Funktionsbegriff vier unterschiedliche Darstellungsweisen von besonderer Bedeutung (vgl. Janvier 1978): So ist es z.B. möglich, einen funktionalen Zusammenhang über eine zugehörige Funktionsgleichung zu beschreiben, was zumindest die prägendste Darstellungsform für ehemalige Schülerinnen und Schüler einer allgemeinbildenden Schule sein dürfte. Man spricht hier von einer formal-symbolischen Darstellung des funktionalen Zusammenhangs. Andererseits bietet der Funktionsgraph (bzw. ein spezieller Ausschnitt davon) eine alternative Repräsentationsform, bei der man von einer graphisch-visuellen Darstellung spricht. Die dritte Form findet man z.B. realisiert in Wertetabellen, die die einzelnen Wertepaare einer Funktion direkt gegenüberstellen. Entsprechend spricht man von einer numerisch-tabellarischen Darstellung. Schlussendlich lässt sich ein funktionaler Zusammenhang noch in seiner vielleicht natürlichsten Weise formulieren: Als Beschreibung des ihm inhärenten und häufig prosaisch formulierten Sachzusammenhangs im Rahmen einer spezifischen Situation, so dass von einer situativ-sprachlichen Darstellung gesprochen wird.

Exemplarisch zeigt Abbildung 3 vier konkrete Darstellungen desselben funktionalen Zusammenhangs. Hierbei lässt sich nur anhand der situativ-sprachlichen Variante erkennen, dass es um die Befüllung eines Kegels mit Wasser geht, während die graphisch-visuelle Form vor allem offenbart, dass die Geschwindigkeit, mit der sich der Kegel füllt, (aufgrund der sich nach oben weitenden Gefäßöffnung) sukzessive abnimmt. Der numerisch-tabellarischen Form lassen sich konkrete Wertepaare schnell entnehmen, so dass für jede Sekunde des Füllprozesses einzelne Füllstände leicht der Tabelle entnommen werden können. Benötigt man jedoch Werte die dazwischen liegen, also z.B. den Füllstand nach 1,5 Sekunden, ist ein Einsetzen in den in formal-symbolischer Form gegebenen Funktionsterm notwendig.

Abb. 3: Derselbe funktionale Zusammenhang in vier verschiedenen Darstellungsformen (entnommen aus Klinger 2018, S. 61)

Je nach individueller Anforderung sind einzelne Informationen zum funktionalen Zusammenhang über die spezifischen Darstellungen als besonders leicht, etwas schwieriger oder aber auch überhaupt nicht zu entnehmen. Erst, wenn alle Darstellungsformen gleichzeitig zur Verfügung stehen, kann man sich ein möglichst umfängliches Bild der zugrundeliegenden Funktion machen.

Gerade aus diesem Grund ist es wichtig, dass Lernende einerseits mit gegebenen Repräsentationen gut umgehen können, was nicht nur das bloße Ablesen von Wertepaaren mit einschließt, sondern vielmehr noch ein flexibles Gespür dafür umfasst, für welche Anforderungen welche Darstellungsformen ihre individuellen Vor- und Nachteile entfaltet. Um diese Intuitionen entwickeln zu können, bedarf es nicht nur, dass sich Schülerinnen und Schüler mit entsprechenden Repräsentationen ausführlich beschäftigen, sondern vor allem auch, dass sie entsprechende Repräsentationen eigenständig konstruieren. Das kann z.B. bedeuten, dass zu einem gegebenen Term eine Wertetabelle erstellt oder zu einem Funktionsgraphen eine Funktionsgleichung gefunden werden muss. In diesem Zusammenhang spricht man dann von einem sog. Repräsentations- oder Darstellungswechsel, den die Lernenden vornehmen müssen.

Solche Darstellungswechsel sind für das Lehren und Lernen von Mathematik von besonderer Bedeutung. Nur, wenn mathematische Konzepte wie jenes der Funktion, aus unterschiedlichen Perspektiven und Blickwinkeln in Form verschiedener Repräsentationsformen für Schülerinnen und Schüler erlebbar gemacht werden, kann sich wirklich ein Blick auf den inhaltlichen Kern eröffnen. In diesem Sinne ist das Greifbarmachen mathematischer Konzepte durch die Verwendung unterschiedlicher Repräsentationsformen ein fundamentaler Bestandteil des Vorstellungsaufbaus im Sinne der oben bereits genauer beschriebenen Grundvorstellungstheorie.

Manche Mathematikdidaktikerinnen und -didaktiker wie etwa Duval (2006) gehen soweit, alles mathematische Arbeiten überhaupt als einzelne Repräsentationswechsel zu betrachten: Formt eine Schülerin etwa den Ausdruck (x+1)² zu x²+2x+1 um, ist sie zwar innerhalb der formal-symbolischen Schreibweise verblieben, hat jedoch eine spezifische Repräsentation durch eine weitere ersetzt, die jedoch zur ersten mathematisch vollständig äquivalent ist und somit auf denselben Inhalt referenziert.

Fehler und Fehlvorstellungen

Umgekehrt werden nicht hinreichend ausgeprägte Grundvorstellungen und eine mangelnde Fähigkeit, mit mathematischen Darstellungen flexibel zu operieren, schnell zum Problem. Das eigentliche Verstehen eines mathematischen Begriffs wie jenem des Funktionsbegriffs kann im Grunde nicht gelingen, wenn Schülerinnen und Schüler einerseits nicht über geeignete Vorstellungen verfügen, die dem zu erlernenden mathematischen Stoff Sinn verleihen, oder nicht in der Lage sind einen Begriff auf verschiedene Weisen durch verschiedene Repräsentationsformen zu greifen.

In Folge solcher Mängel lassen sich häufig verschiedene Fehlermuster beobachten. An dieser Stelle muss jedoch vorsichtig unterschieden werden: Im normalen Fall handelt es sich um einen Flüchtigkeits-, Rechenfehler oder einen Fehler im Rahmen einer ersten Aneignung eines mathematischen Konzepts, der vermutlich bei einer erneuten Betrachtung einer Aufgabe durch den Lernenden selbst korrigiert werden kann bzw. durch sinnvolles Üben und Vertiefen beseitigt würde. Die Alternative ist ein tiefer gelagertes und möglicherweise nur schwer aufzulösendes Missverständnis, dessen Ursache in unzureichend oder falsch ausgebildeten Vorstellungen liegt. In diesem zweiten Fall wird in der Mathematikdidaktik meist von sog. Fehlvorstellungen gesprochen, die bereits im Planungsprozess von Unterricht mitgedacht und denen idealerweise frühzeitig entgegengewirkt wird. Während im Kopf des Lernenden verankerte Fehlvorstellungen schnell zu Fehlern, etwa im Bearbeitungsprozess von Aufgaben führen, lässt sich also längst nicht jeder Fehler auf ein solches systematisches Muster zurückführen. Im Gegenteil: Fehler sind notwendiger und sinnvoller Bestandteil eines jeden Aneignungsprozesses.

Illusion von Linearität

Hierbei sind die Unterschiede zwischen einfachen Fehlern und verfestigten Fehlvorstellungen häufig schwer auszumachen. Dies lässt sich beispielsweise am Fehlertyp der sog. „Illusion von Linearität“ (engl. „Illusion of Linearity“), auf welchen bereits oben kurz eingegangen wurde, erläutern. Gemeint ist hierbei, dass Lernende aber auch im Allgemeinen Menschen überhaupt dazu neigen, funktionale Zusammenhänge als linear anzunehmen und dies auch dann, wenn andere Ansätze mehr Erfolg versprechen oder lineare sogar zu merkbar falschen Resultaten führen. Linearität zeichnet sich mathematisch als konstantes Wachsen aus, die abhängige Größe ergibt sich aus der unabhängigen Größe jeweils durch die Multiplikation mit einem festen Faktor. Damit wird der Zusammenhang durch eine Funktionsgleichung der Form f(x)= ax mit einem solchen Faktor a beschrieben.

Tatsächlich bietet unser Alltag eine Vielzahl an beispielhaften Zusammenhängen, die einer solchen Gesetzmäßigkeit unterliegen: Etwa der Zusammenhang zwischen der Anzahl eines gekauften Artikels und dem davon abhängigen Gesamtpreis, die Länge einer Reisestrecke und der davon abhängige Verbrauch des verwendeten Kraftstoffs oder die Arbeitszeit eines Arbeiters und die davon abhängige Anzahl gefertigter Produkte. In all diesen Fällen bildet die Annahme einer zugrundeliegenden linearen Funktion die einfachste Möglichkeit, ein Modell aufzustellen um Vorhersagen zu treffen.

Aber so leicht ist es nicht immer: Beim Wareneinkauf gibt es Mengenrabatte oder Abnahmebeschränkungen, bei der Autoreise kann man sich verfahren oder unterliegt verkehrsbedingten Geschwindigkeitsschwankungen und ein Arbeiter dürfte nach einer Weile Ermüdungserscheinungen zeigen und somit nicht stets mit einheitlicher Effizienz arbeiten. Entsprechend reicht in vielen Fällen und insbesondere dann, wenn höhere Präzision und eine damit verbundene größere Aussagekraft notwendig ist, ein linearer Modellansatz nicht mehr aus.

In solchen Fällen müssen auch Schülerinnen und Schüler in der Lage sein, den Blick zu weiten und nicht auf einem linearen Ansatz zu verharren. Dass dies jedoch in vielen Situationen der Fall ist, haben insbesondere die bereits oben erwähnten belgischen Forscher De Bock, Van Dooren, Janssens und Verschaffel gezeigt (z.B. De Bock et al. 2007). Die vorgestellte Aufgabe zur Vergrößerung des Weihnachtsmannbildes ist leider nur ein Beispiel unter vielen. Und stets müssen Schülerinnen und Schüler zur Lösung die Art des zugrundeliegenden funktionalen Zusammenhangs erschließen. Bei der gezeigten Aufgabe sind die benötigten Informationen in einer situativ-verbalen Beschreibung gebunden und müssen aus dieser entnommen werden. Da einerseits die Wertepaare konkret einander zugeordnet werden aber auch die Qualität des zugrundeliegenden Zusammenhangs ausgemacht werden muss, stehen sowohl Zuordnungs- als auch Kovariationsvorstellung bei diesem Item in besonderem Fokus, während der funktionale Zusammenhang als Ganze kaum in den Vordergrund tritt.

Wer als Antwort „18 ml“ nennt, ist also mit großer Wahrscheinlichkeit von einem hier unpassenden linearen Zusammenhang ausgegangen und somit einer Illusion von Linearität erlegen. In diesem Fall wurde also die Art des zugrundeliegenden funktionalen Zusammenhangs nicht korrekt identifiziert. Natürlich ist diese Aufgabe auch stark suggestiv. Es kann nicht automatisch von einer Fehlvorstellung in obigem Sinne ausgegangen werden, da es sich eben auch um einen schlichten Flüchtigkeitsfehler handeln kann.

Nichtsdestotrotz setzten bei den Lernenden erst nachdem durch die Forscher ein kognitiver Konflikt erzeugt wurde, ein steigender Grad an Sicherheit und erste Reflexionsprozesse ein: So ist es z.B. ersichtlicher, dass der angegebene Wert nicht zutreffen kann, wenn man sich rechteckige Rahmen um die beiden verschieden großen Darstellungen vorstellt. Mit einer entsprechenden Variante der Abbildung konnten De Bock et al. manchen Schülerinnen und Schülern so eine geeignete Unterstützung anbieten, das Problem noch korrekt zu lösen und von der Annahme eines linearen Zusammenhangs abzusehen.

Was können Schülerinnen und Schüler wirklich?

Insgesamt gibt es einige Untersuchungen, die jener von De Bock et al. ähnlich sind. Meist zielen sie darauf ab, in kleinen Interviewsettings Einsicht in das Denken und Handeln von Lernenden zu erhalten. Geeignete Testinstrumente, die auch eine Erhebung mit sehr großen Fallzahlen zulassen, frei zugänglich und speziell auf die Erhebung des Fähigkeitsstandes von Schülerinnen und Schülern im Bereich von Funktionen und des Funktionalen Denkens sind, standen zu Beginn des Projekts FALKE (Funktionales Denken und frühe Analysis: Lernen von Konzepten in der Einführungsphase; siehe z.B. www.falke-test.de) nur unzureichend zur Verfügung.

Im Rahmen des Projekts FALKE konnte ein solches Testinstrument entwickelt werden, welches im Speziellen verstehensorientierte Elemente der Funktionenlehre und frühen Analysis fokussiert. Während der erste Begriff vor allem auf das Thema „Funktionen“ im Bereich der Sekundarstufe I abzielt, bezeichnet „Analysis“ vor allem die Differential- und Integralrechnung der Oberstufe, die natürlich auf einem durch den Funktionsbegriff der Sekundarstufe I gebildeten Fundaments fußt. Mit „früher Analysis“ ist dann vor allem das erste Jahr der Einführung und somit insbesondere ein erstes Bild der Ableitungsfunktion gemeint.

Die Testaufgaben (sog. Items) sind so konstruiert, dass Lernende entsprechende (Grund-)Vorstellungen der entsprechenden Inhalte ausgebildet haben müssen, aber auch mit den entsprechenden Repräsentationsformen flexibel umgehen können müssen. Zudem bieten die Items an einigen Stellen die Möglichkeit typische Fehler zu begehen und geben so Einsicht in die Fähigkeitsstruktur der Schülerinnen und Schüler und etwaig vorhandener Fehlvorstellungen (vgl. Klinger 2018).

Insgesamt konnte der Test über 3000 Schülerinnen und Schülern im Schuljahr 2014/15 vorgelegt werden, die ihrerseits von etwa 150 Lehrkräften unterrichtet wurden. Die Stichprobe bestand aus Lernenden der nordrhein-westfälischen Einführungsphase und somit dem ersten Jahr der Oberstufe an Gymnasien, Gesamtschulen und Beruflichen Gymnasien. Insgesamt hatten die Probanden der Studie 45 Minuten Zeit, um das in klassischer Paper-and-Pencil-Form vorgelegte Testheft zu bearbeiten (vgl. Klinger 2018, S. 207 ff.).

Quantifizierung entsprechender Fehlermuster

Im Rahmen der Studie wurde so auch die bereits oben vorgestellte Aufgabe (siehe erneut Abbildung 1) den Schülerinnen und Schülern der Stichprobe vorgelegt. Hierbei gaben 77,7 Prozent der Probanden die Antwort „18 ml“. Lediglich 3,4 Prozent der Schülerinnen und Schüler lösten das Item korrekt. Der restliche Anteil entfiel auf übrige Antworten bzw. auf Bearbeitungen, bei denen zwar Rechnungen der Lernenden aber kein Ergebnis dieser erkennbar waren. Insgesamt erwies sich das Item somit für die beteiligten Schülerinnen und Schüler als nur schwer lösbar.

Ein weiteres Item des Testinstruments ist in Abbildung 4 dargestellt. Auch hier steht wieder ein funktionaler Zusammenhang im Mittelpunkt. Anders als bei der zuvor betrachteten Aufgabe muss hier keine Zahl berechnet werden, sondern ein Funktionsgraph in qualitativ korrekter Weise skizziert werden. Dieser liegt wieder gebunden in einer situativ-verbalen Beschreibung vor, welche durch eine kleine Skizze unterstützt wird. Ähnlich ist auch hier, die Art und Weise wie Zuordnungs- und Kovariationsvorstellung im Vordergrund stehen.

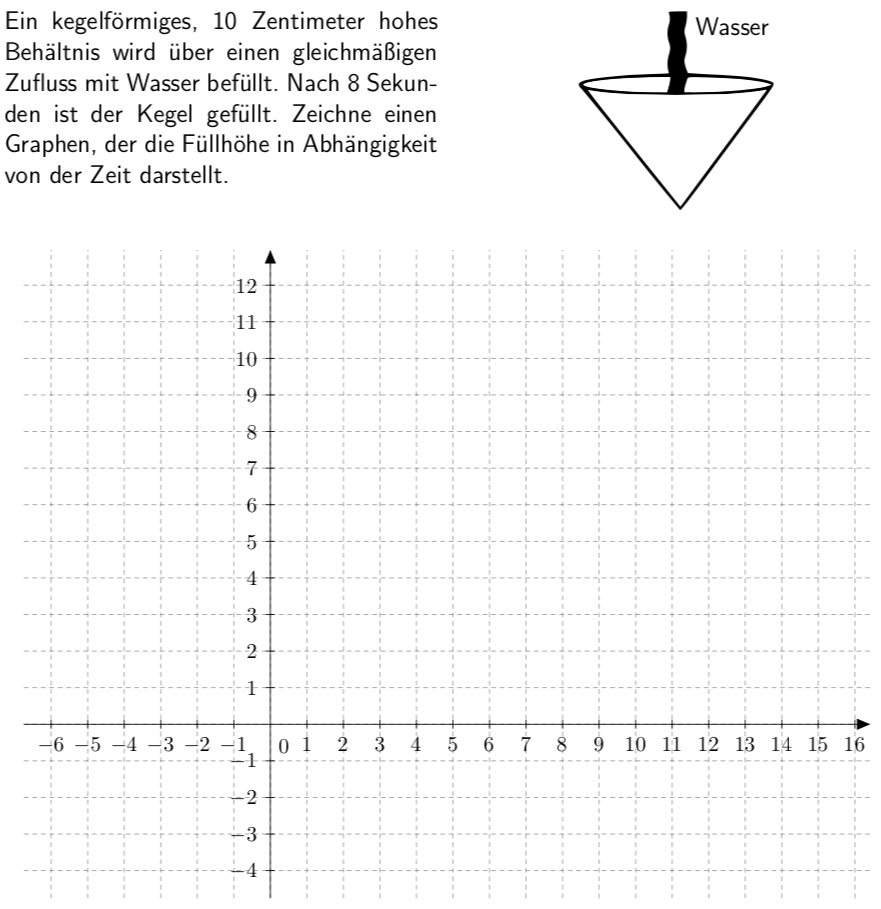
Abb. 4: Aufgabe „Kegelfüllung“ des FALKE-Tests (entnommen aus Klinger 2018, S. 247)

Konkret geht es um die Frage, wie ein Graph aussehen kann, der die Füllhöhe eines kegelförmigen Behältnisses in Abhängigkeit von der vergangenen Zeit beschreibt, wobei über einen gleichmäßigen Zufluss Wasser hineingegeben wird.

In Abbildung 5 sind hierzu zwei exemplarische Schülerbearbeitungen dargestellt. Während der Urheber der linken Lösung erkannt hat, dass aufgrund der Form des Gefäßes die Zunahmerate der Füllhöhe im Verlauf des Prozesses sukzessive abnimmt und somit die Qualität des zugrundeliegenden funktionalen Zusammenhangs korrekt einschätzt, gelingt dies einigen Schülerinnen und Schülern, die für solche Bearbeitungen wie den rechten Lösungsversuch verantwortlich sind, nicht. Ihre Vorstellungen werden von einem Zusammenhang von linearer Gestalt dominiert und so zeichnet sie jenen Graphen, der im Kontext des vorliegenden Items auf eine Illusion von Linearität zielt.

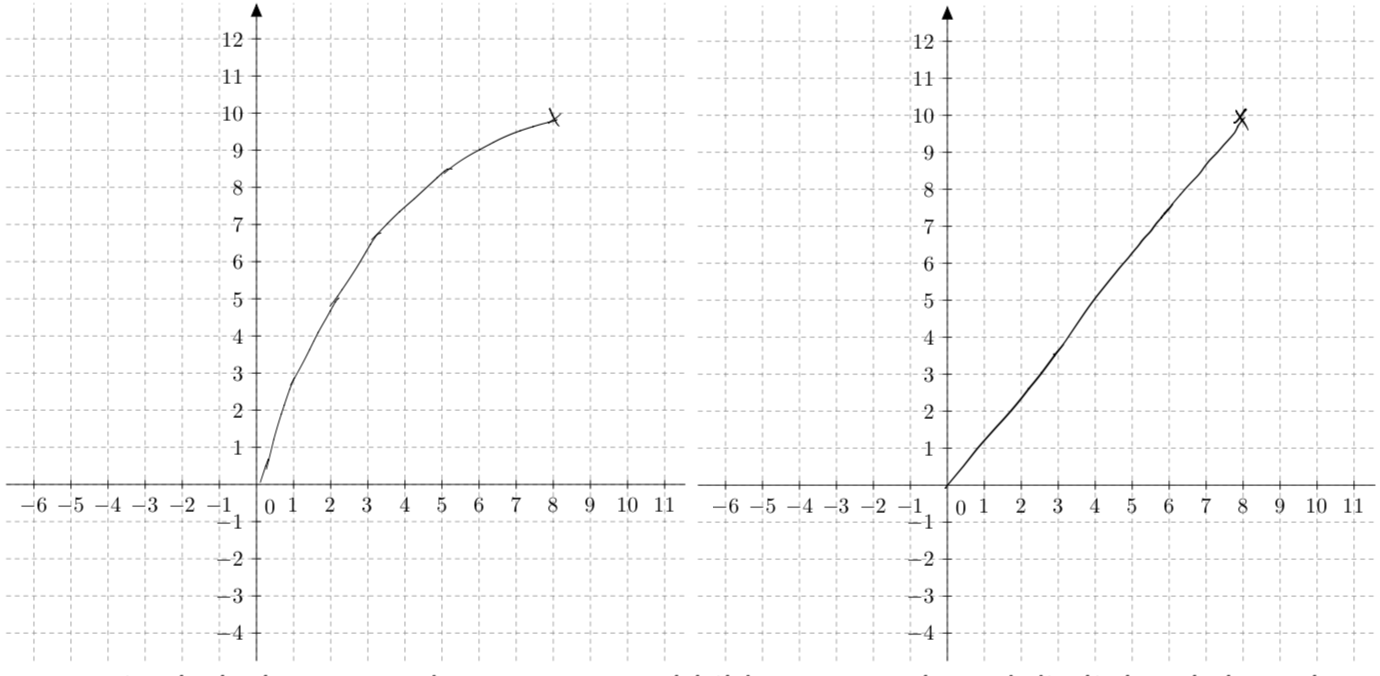
Abb. 5: Zwei Schülerlösungen des Items aus Abbildung 4. Während die linke als korrekt gewertet wurde, handelt es sich bei der rechten um eine Fehlbearbeitung.

Insgesamt wurde das Item von 38,3 Prozent der teilnehmenden Schülerinnen und Schüler korrekt bearbeitet. Mit 26,1 Prozent wies jedoch über ein Viertel der erfassten Stichprobe eine besondere mentale Dominanz linearer Zusammenhänge auf, zeichnete also einen Graphen ähnlich zu jenem in Abbildung 5 rechts (vgl. Klinger 2018, S. 249 ff.).

Insgesamt lässt sich das Fehlermuster „Illusion von Linearität“ also in sehr unterschiedlichen Aufgabenformaten und damit verbunden verschiedenen mathematischen Tätigkeiten beobachten. Während im ersten betrachteten Item also etwa Dreiviertel der Probanden ein Fehlermuster zeigen, das in Richtung einer Übergeneralisierung linearer Zusammenhänge deutet, zeigt sich für das zweite Item ein zwar immer noch erheblicher jedoch deutlich geringerer Anteil von etwa einem Viertel. Insgesamt zeigen die durch die Studie gewonnenen Daten, die sich noch auf weitere Items beziehen, dass die Quote die auf das entsprechende Fehlermuster entfällt, stark vom jeweiligen Item und somit auch vom betrachteten Aufgabenformat abhängt. Dies lässt sich u.a. auf die teils deutlich unterschiedliche Suggestivität, die Art des erforderten Darstellungswechsels sowie die im Fokus stehenden Grundvorstellungen der jeweils betrachteten Items zurückführen (vgl. Klinger 2018, S. 359 ff.).

Graph als Bild

Im Rahmen der Entwicklung und Durchführung des FALKE-Tests wurde nicht nur das Fehlermuster „Illusion von Linearität“ in den Blick genommen. Ein anderer Fehlertyp ist etwa noch der sog. Graph-als-Bild-Fehler, welcher seinem Namen entsprechend vor allem die Darstellung einer Funktion in Form ihres Graphs betrifft. Hierbei interpretieren Schülerinnen und Schüler einen solchen Funktionsgraphen nicht als Menge aller durch einen funktionalen Zusammenhang gegebenen Wertepaare, sondern fassen ihn als unmittelbares fotografisches Abbild einer gegebenen Situation auf.

Als Beispiel ist in Abbildung 6 ein weiteres Item des FALKE-Tests dargestellt. Die Lernenden müssen wieder eine situativ-verbale Beschreibung, in der ein funktionaler Zusammenhang zumindest qualitativ gekapselt ist, in einen Funktionsgraphen überführen. Diesmal jedoch muss kein Funktionsgraph gezeichnet, sondern nur einer von vier möglichen als der Situation angemessen erkannt werden.

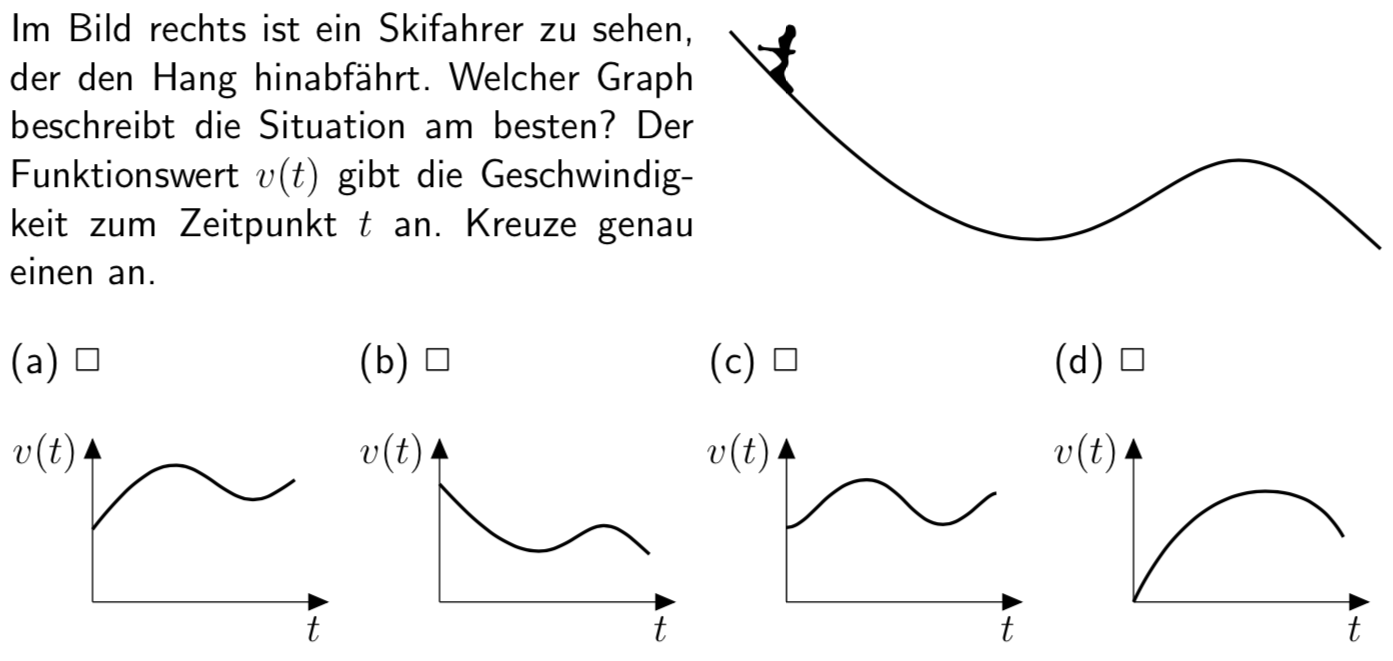
Abb. 6: Aufgabe „Skifahrer“ des FALKE-Tests (angelehnt an Nitsch 2015, S. 234)

Die Bewegung des dargestellten Skifahrers muss der beschriebenen Situation und insbesondere der längsschnittlichen Skizze entnommen und auf einen Geschwindigkeits-Zeit-Graphen übertragen werden. Während seiner Abfahrt wird der Wintersportler zunächst an Geschwindigkeit gewinnen, verliert dann durch den kleinen Hügel an Fahrt, bis er anschließend sein Tempo wieder erhöht. Dies gibt Variante (a) am besten wieder, so dass Probanden hier ihr Kreuz setzen müssen, damit das Item als korrekt bearbeitet gewertet wird.

Insgesamt zeigt sich das Item (natürlich auch aufgrund der gegebenen Wahrscheinlichkeit eines Rateerfolgs) im Vergleich zu den anderen hier abgebildeten Aufgaben als eher einfach. 68,5 Prozent der Probanden der Stichprobe konnten es zu unserer Zufriedenheit bearbeiten, 17,4 Prozent entfallen auf Antwortmöglichkeit (b), 8,6 Prozent auf Möglichkeit (c) und 5,6 Prozent auf Möglichkeit (d).

Dass Variante (b) die häufigste Falschantwort darstellt, ist kein Zufall: Sie steht für den Graph-als-Bild-Fehler. Bei der abgebildeten Kurve handelt es sich um eine exakte Kopie der dargestellten Skizze, so dass davon auszugehen ist, dass Schülerinnen und Schüler, die sich für diesen Distraktor entscheiden, ihn wie oben beschrieben als ein unmittelbares fotografisches Abbild der gegebenen Situation auffassen. Natürlich lässt sich aber auch hier nicht sicher sagen, ob eine entsprechende Auswahl eines Probanden auf tiefsitzende Fehlverständnisse zurückzuführen oder schlicht der Prüfungssituation und einer damit verbundenen Unachtsamkeit geschuldet sind.

Während sich die Fehlermuster hinsichtlich der Quantität ihres Auftretens von Item zu Item, wie oben beschrieben, als durchaus divers zeigen, gilt dies für dasselbe Item, das unterschiedlichen Stichproben vorgelegt wird, im Übrigen nicht: Obwohl Nitsch (2015) in ihrer Studie das Item Schülerinnen und Schülern eines anderen Bundeslandes und teilweise sogar anderer Schulformen vorlegte, ergibt sich ein durchaus vergleichbares Bild: So wählten hier 66,1 Prozent der Probanden die korrekte Lösung (a), während sich mit einem Anteil von 19,3 Prozent ähnlich viele Lernende für die Antwortmöglichkeit entschieden, die dem Graph-als-Bild-Fehler entspricht (vgl. Klinger 2018, S. 262 f.).

Fazit

Im Rahmen des FALKE-Forschungsprojekts konnte ein fundiertes Testinstrument entwickelt werden, das nun auch für weitere Studien eingesetzt werden kann. Das Instrument haben wir unter einer freien Creative Commons-Lizenz zum kostenlosen Download veröffentlicht, so dass Sie sich auch selber ein Bild des gesamten Tests machen können (siehe www.falke-test.de).

Durch unsere Stichprobe von über 3000 Schülerinnen und Schülern aus Nordrhein-Westfalen wird uns ein breiter Blick in das Fähigkeitsspektrum der Lernenden eröffnet. Hierbei lässt sich ein unterschiedlicher Grad an ausgebildeten Grundvorstellungen, eine verschiedentliche Versiertheit mit mathematischen Darstellungsformen und vielfältige Fehlertypen im Themenfeld funktionaler Zusammenhänge und früher Analysis beobachten.

Obwohl viele dieser Fehler in teils beträchtlichem Ausmaße beobachtet werden konnten, soll aber kein zu negatives Bild gezeichnet werden: Fehler sind Bestandteil des Lernprozesses und stellen teils notwendige Hürden in seinem Verlauf dar. Schülerinnen und Schüler befinden sich mitten in diesem Lernprozess und blicken auf mehr als zwei noch folgende Jahre bis zum Abitur. Es bleibt also genug Zeit die spezifischen Hürden zu nehmen.

Damit dies gelingen kann, ist die Ausrichtung des Mathematikunterrichts von entscheidender Bedeutung: So müssen angeregte (Grund-)Vorstellungen bei der Entwicklung, Durchführung und Reflexion des Unterrichts mitgedacht werden, vielfältige Darstellungstypen angeboten und miteinander vernetzt sowie die unterschiedlichen Fehlertypen gezielt aufgegriffen werden. So wird etwa in der Schulbuchreihe „mathewerkstatt“ im Cornelsen-Verlag, welche von Bärbel Barzel mitherausgegeben wird, jedes mathematische Thema durch konkrete lebensweltliche Bezüge motiviert und essentiell auf die Vernetzung der zuvor genannten Aspekte gesetzt. Auf diese und ähnliche Weise kann ein Bild von Mathematik vermittelt werden, dass auch abseits stupider Regelausführung spannende und sinnstiftende Erlebnisse mathematischer Inhalte bereithält, so dass sich den Lernenden der Sinn der jeweiligen mathematischen Konzepte offenbart. Auf diese Weise soll letztlich mehr in Erinnerung bleiben als ein Symbol, so dass f(x) nicht nur irgendetwas ist, in das man einsetzt, sondern etwas, wohinter sich ein breites von Verständnis gezeichnetes Bild verbirgt.

Literatur

• Barzel, Bärbel, Leuders, Timo, Prediger, Susanne, Hußmann, Stephan: Designing tasks for engaging students in active knowledge organization, in C. Margolinas (Hrsg.): Task design in mathematics education, Proceedings of ICMI Study 22, Oxford 2013, 285–294.
• De Bock, Dirk, Van Dooren, Wim, Janssens, Dirk, Verschaffel, Lieven: The illusion of linearity, From analysis to improvement, New York, Springer, 2007
• Duval, Raymond: A cognitive analysis of problems of comprehension in a learning of mathematics, in Educational Studies in Mathematics, 61(1–2)/2006, 103–131
• Ganter, Sandra: Experimentieren – ein Weg zum Funktionalen Denken, Empirische Untersuchung zur Wirkung von Schülerexperimenten, Hamburg, Kovač, 2013
• Janvier, Claude: The interpretation of complex cartesian graphs representing situations, Studies and teaching experiments, University of Nottingham, Nottingham, 1978
• Klinger, Marcel: Funktionales Denken beim Übergang von der Funktionenlehre zur Analysis, Entwicklung eines Testinstruments und empirische Befunde aus der gymnasialen Oberstufe, Springer Spektrum, Wiesbaden, 2018
• Krüger, Katja: Erziehung zum funktionalen Denken, Zur Begriffsgeschichte eines didaktischen Prinzips, Logos, Berlin, 2000
• KMK (Sekretariat der Ständigen Konferenz der Kultusminister der Länder der Bundesrepublik Deutschland): Bildungsstandards im Fach Mathematik für den Mittleren Schulabschluss, Beschluss vom 4.12.2003, Luchterhand, München, 2004
• Malle, Günther: Zwei Aspekte von Funktionen, Zuordnung und Kovariation, in Mathematik Lehren, 103/2000, 8–11
• Nitsch, Renate: Diagnose von Lernschwierigkeiten im Bereich funktionaler Zusammenhänge, Eine Studie zu typischen Fehlermustern bei Darstellungswechseln, Springer Spektrum, Wiesbaden, 2015
• Theyßen, Heike:  Mythos Bierschaumzerfall, Ein Analogon für den radioaktiven Zerfall?, in Physik und Didaktik in Schule und Hochschule, 8(2)/2009, 49–57
• Vollrath, Hans-Joachim: Funktionales Denken, in Journal für Mathematik-Didaktik, 10(1)/1989, 3–37
• Vollrath, Hans-Joachim: Funktionale Zusammenhänge, in Linneweber-Lammerskitten, Helmut (Hrsg.): Fachdidaktik Mathematik, Grundbildung und Kompetenzaufbau im Unterricht der Sek. I und II, Kallmeyer, Seelze 2014, 112–125
• vom Hofe, Rudolf: Grundvorstellungen mathematischer Inhalte, Spektrum, Heidelberg, 1995

(unredigierte Fassung; erschien in: Klinger, M. & Barzel, B. (2019). Der Funktionsbegriff: Zur Illusion von Linearität und anderen Hürden beim Funktionalen Denken. Unikate: Berichte aus Forschung und Lehre, Heft 53, 35–46.)