Marcel Klinger & Bärbel Barzel

Im Rahmen der Dissertation von Klinger (2018) wurde das FALKE-Testinstrument entwickelt (Funktionales Denken und Analysis – Lernen von Konzepten in der Einführungsphase, s. z.B. www.falke-test.de), welches das Schülerverständnis von Konzepten im ersten Jahr der Oberstufe (in Nordrhein-Westfalen die sog. Einführungsphase) fokussiert. Der Test befindet sich inhaltlich somit an der Nahtstelle zwischen der Funktionenlehre der Sekundarstufe I und der frühen Analysis samt des Differentialrechnungskonzepts der Oberstufe. Gerade für die Sekundarstufe werden im Rahmen von Meta-Studien mathematischen Leistungstests häufig geschlechtsspezifische Effekte zu Gunsten des männlichen Geschlechts attestiert (z.B. Hyde et al. 1990; Lindberg et al. 2010), so dass die Thematik auch für die vorliegende Studie eine besondere Bedeutung hat.

Mathematische Leistungstests und Geschlecht

Nach Klieme (1986, S. 133) gehören geschlechtsspezifische Leistungsdispositionen bzgl. gemessener Mathematikleistung zu den „am deutlichsten ausgeprägten und am besten dokumentierten Befunden über Geschlechterunterschiede im Bereich der Psychologie“ überhaupt. Entsprechende Effekte (z.B. bestimmt durch Cohens d) fallen üblicherweise nahe bei null bis mittelstark aus, erreichen jedoch häufig ein zu Gunsten des männlichen Geschlechts signifikantes Niveau und nehmen typischerweise im Verlauf der Schullaufbahn sukzessive zu (Hyde et al. 1990; Lindberg et al. 2010). Ist ein Test besonders rechenintensiv oder kalkülhaltig, fallen die Effekte geringer aus oder kehren sich sogar zu Gunsten des weiblichen Geschlechts um (Hyde et al. 1990).

Die Ursachen der in zahlreichen Studien ermittelten geschlechtsspezifischen Unterschiede sind nicht endgültig geklärt. So fassen etwa Köller & Klieme (2000) eine Vielzahl verschiedener Erklärungsansätze zusammen und ordnen diese in vier Kategorien: biologische Erklärungsansätze (z.B. aufgrund eines unterschiedlichen Selektionsdrucks bei Männern und Frauen), kognitive Erklärungsansätze (z.B. unterschiedliche Fähigkeiten bzgl. der Raumvorstellung), psychosoziale Erklärungsansätze (z.B. aufgrund verfestigter Geschlechterstereotype innerhalb der häuslichen Umwelt) sowie unterrichtsbezogene Erklärungsansätze (z.B. in Form ungleicher Behandlung durch die Lehrkraft oder unterschiedlich stark ausfallender lebensweltlicher Bezüge in Schulbüchern und Curricula) (vgl. auch Klinger 2018, S. 170 ff.).

Testkonzeption und Erhebung

Das Testinstrument ist so konzipiert, dass ein erster Teiltest zu Beginn, ein zweiter gegen Ende der Einführungsphase eingesetzt werden kann. Entsprechend wurden Items so entwickelt, dass sie den spezifischen curricularen Anforderungen genügen: Während die Items des ersten Tests sich daher auf die Funktionenlehre der Sekundarstufe I beschränken, umfasst der zweite Test auch Items, die die formal erst gegen Ende der Einführungsphase zur Verfügung stehenden Konzepte, wie etwa die ersten Begriffe der Differentialrechnung, adressieren. Neben der Fokussierung unterschiedlicher Grundvorstellungen hat vor allem der flexible Umgang mit unterschiedlichen Darstellungsformen sowie insbesondere deren Wechsel eine besondere Bedeutung für die Tests und den durch sie operationalisierten Verständnisbegriff. Eine genauere Erläuterung findet sich in Klinger & Barzel (2018).

Im Schuljahr 2014/15 wurden die FALKE-Tests großflächig im Raum Nordrhein-Westfalen eingesetzt. Hierbei konnten für den ersten insgesamt 3202 (50.0% w., 49.5% m.), für den zweiten Test insgesamt 2665 (48.9% w., 50.3% m.) Schülerinnen und Schüler erfasst werden.

Analyse der Erhebungsdaten bzgl. des Einflussfaktors Geschlecht

Insgesamt ergibt sich für beide Tests eine Effektstärke zu Gunsten der männlichen Probanden zwischen 0,37 und 0,38 (vgl. Klinger 2018, S. 388 ff.). Hierbei zeichnet eine itemweise Betrachtung jedoch ein weniger einheitliches Bild (s. Abbildung 1): Zwar ergibt sich für alle Items des ersten Tests jeweils ein (teilweise nicht signifikanter) Leistungsvorteil zu Gunsten der Jungen, jedoch hängt dieser gemessen an der Differenz der Lösungsquote innerhalb der nach Geschlecht getrennten Teilstichprobe stark vom jeweils betrachteten Item ab. Während sich für Item L4MB eine vernachlässigbare Differenz von 0,3 Prozentpunkten ergibt, zeigt sich für Item J9SD mit 19,7 Prozentpunkten ein bedeutend größerer Effekt. Item N1FQ zeigt mit 10,8 Prozentpunkten Differenz den zweitstärksten Effekt. Zusätzlich ist das Verhältnis RR von Lösungsquote der männlichen und Lösungsquote der weiblichen Substichprobe (sog. relatives Risiko) angegeben. Hier zeigt sich Item H7ZD als besonders auffällig.

Ein ähnliches Bild ergibt sich auch auf Itemebene bei der Betrachtung des zweiten Tests. Im Unterschied zum ersten Test fallen hier jedoch auch Items zu Gunsten des weiblichen Geschlechts aus, dies jedoch mit vernachlässigbarer bzw. kaum signifikanter Effektstärke. Insgesamt lässt sich für beide Tests beobachten, dass vor allem eher kalkülhafte Items geringe bis keine geschlechtsspezifischen Differenzen bzgl. der Lösungsquote aufweisen. Für weitere Details sei auf Klinger (2018, S. 393 ff.) verwiesen.

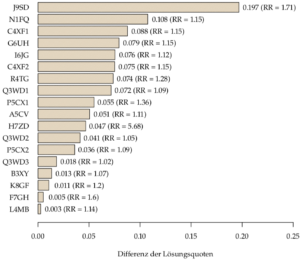
Abb. 1: Itemweise Übersicht der geschlechtsspezifischen Effekte für den ersten Test

Füllgraphen und die Illusion of Linearity

Abbildung 2 zeigt Item J9SD samt zweier Schülerbearbeitungen. Das Item verlangt einen Darstellungswechsel eines funktionalen Zusammenhangs von der situativ-sprachlichen zur graphisch-visuellen Darstellungsform. Hierbei liegt aufgrund der Kegelform des Gefäßes ein funktionaler Zusammenhang zugrunde, der nicht linear ist, sondern stetig an Wachstumsgeschwindigkeit verliert. Entsprechend handelt es sich bei der Lösung unten rechts um eine korrekte, bei der Lösung unten links um eine Falschbearbeitung, die sich durch eine Übergeneralisierung linearer Zusammenhänge auszeichnet. Liegt eine konkrete Fehlvorstellung zugrunde, wird in diesem Zusammenhang oft von einer sog. Illusion of Linearity gesprochen (De Bock et al. 2007).

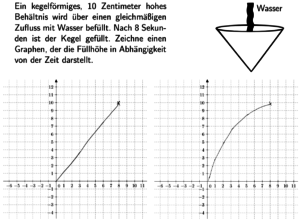
Abb. 2: Aufgabenstellung zu Item „Kegelfüllung“ (J9SD) (oben Mitte) sowie Beispiele für eine Fehl- (unten links) wie korrekte Bearbeitung (unten rechts)

Während das Item von 47,5% der männlichen Probanden korrekt bearbeitet wird, können es nur 27,8% der Testteilnehmerinnen fehlerfrei lösen. Umgekehrt zeichnen jedoch 27,3% der Mädchen eine lineare Funktion wie abgebildet. Unter dem männlichen Teil der Stichprobe war dieses Fehlermuster mit 16,1% deutlich weniger prominent. Ähnliche Darstellungswechsel werden auch durch die Items N1FQ und H7ZD gefordert. Beide Items begünstigen in ihrer Anlage zudem das Fehlermuster „Illusion of Linearity“.

Fazit

Insgesamt lassen sich deutliche Vorteile zu Gunsten der männlichen Probanden feststellen. Die Effekte schwanken unter den Items jedoch teilweise stark. Items, die besonders auf das Fehlermuster „Illusion of Linearity“ zugespitzt sind, zeigen sich auffällig hinsichtlich geschlechtsspezifischer Effekte. Zudem sind Items, die den Darstellungswechsel zwischen einer Situation und einem Funktionsgraphen (insbesondere vor dem Kontext von Füllgraphen) erfordern, besonders betroffen. Das beschriebene Forschungsprojekt beleuchtet somit ein Phänomen, zu dessen Ursachen derzeit noch keine fundierten Aussagen gemacht werden können. Dies ist als Forschungsdesiderat für weitere Studien zu verstehen.

Literatur

• De Bock, D., Van Dooren, W., Janssens, D. & Verschaffel, L. (2007). The illusion of linearity: From analysis to improvement. New York: Springer.
• Hyde, J. S., Fennema, E. & Lamon, S. J. (1990). Gender differences in mathematics performance: A meta-analysis. Psychological Bulletin, 107(2), 139–155.
• Klieme, E. (1986). Zur Problematik geschlechtsspezifischer Mathematikleistungen. In H.-G. Steiner (Hrsg.), Grundfragen der Entwicklung mathematischer Fähigkeiten (S. 133–151). Köln: Aulis Deubner.
• Klinger, M. (2018). Funktionales Denken beim Übergang von der Funktionenlehre zur Analysis: Entwicklung eines Testinstruments und empirische Befunde aus der gymnasialen Oberstufe. Wiesbaden: Springer Spektrum.
• Klinger, M. & Barzel, B. (2018). Zielgerichtete Entwicklung von verstehensorientierten Leistungstestaufgaben am Beispiel des Funktionalen Denkens in der frühen Analysis der Oberstufe. In Beiträge zum Mathematikunterricht 2018. Münster: WTM.
• Köller, O. & Klieme, E. (2000). Geschlechtsdifferenzen in den mathematisch-naturwissenschaftlichen Leistungen. In J. Baumert, W. Bos & R. Lehmann (Hrsg.), TIMSS/III: Dritte Internationale Mathematik- und Naturwissenschaftsstudie – Mathematische und naturwissenschaftliche Bildung am Ende der Schullaufbahn (Bd. 1, S. 373–404). Opladen: Leske+Budrich.
• Lindberg, S. M., Hyde, J. S., Petersen, J. L. & Linn, M. C. (2010). New trends in gender and mathematics performance: A meta-analysis. Psychological Bulletin, 136(6), 1123–1135.

(erschienen in: Klinger, M. & Barzel, B. (2018). Zum Einfluss des Geschlechts beim Darstellungswechsel funktionaler Zusammenhänge. In Fachgruppe Didaktik der Mathematik der Universität Paderborn (Hrsg.), Beiträge zum Mathematikunterricht 2018 (Bd. 2, S. 149–152). Münster: WTM-Verlag. – DOI: 10.17877/DE290R-19458)